题目内容
6.关于x的一元二次方程x2-mx-1=0的两个实数根分别是x1、x2,且x12+x22=7,则(x1-x2)2的值是29.分析 首先根据根与系数的关系,得出x1+x2和x1x2的值,然后根据x12+x22的值求出m(需注意m的值应符合此方程的根的判别式);然后再代值求解.
解答 解:由题意,得:x1+x2=m,x1x2=-1;
则:(x1+x2)2=x12+x22+2x1x2,
即m2=7+2(-1)=5,
解得m=±5;
当m=5时,x1+x2=5,x1x2=1;
∴(x1-x2)2=(x1+x2)2-4x1x2=29,
当m=-5时,x1+x2=-5,x1x2=-1;
∴(x1-x2)2=(x1+x2)2-4x1x2=29,
则(x1-x2)2的值是29,
故答案为:29.
点评 本题考查了根与系数的关系、根的判别式、完全平方公式等知识.本题需注意的是在求出m值后,一定要用根的判别式来判断所求的m是否符合题意,以免造成多解、错解.

练习册系列答案
相关题目
16. 平行四边形ABCD中,对角线AC、BD交于点O,点E是BC的中点.若OE=3cm,则AB的长为( )
平行四边形ABCD中,对角线AC、BD交于点O,点E是BC的中点.若OE=3cm,则AB的长为( )
 平行四边形ABCD中,对角线AC、BD交于点O,点E是BC的中点.若OE=3cm,则AB的长为( )
平行四边形ABCD中,对角线AC、BD交于点O,点E是BC的中点.若OE=3cm,则AB的长为( )| A. | 3cm | B. | 6cm | C. | 9cm | D. | 12cm |
17.公园门票价格规定如下表:
甲、乙两个班共104人去游公园,其中甲班人数较少.如果两个班分别购票,则一共应付1240元,
(1)两班各有多少学生?
(2)如果两班联合起来,作为一个团体购票,可省多少钱?
(3)如果甲班单独组织去游公园,作为组织者,你将如何安排购票才最省钱?
| 购票张数 | 1~50 | 51~100 | 100以上 |
| 每张票的价格 | 13元 | 11元 | 9元 |
(1)两班各有多少学生?
(2)如果两班联合起来,作为一个团体购票,可省多少钱?
(3)如果甲班单独组织去游公园,作为组织者,你将如何安排购票才最省钱?
1.解下列方程,最适合用公式法求解的是( )
| A. | (x+2)2-16=0 | B. | (x+1)2=4 | C. | $\frac{1}{2}$x2=1 | D. | x2-3x-5=0 |
11.下列运算正确的是( )
| A. | 2x+3y=5xy | B. | 3x2y-5xy2=-x2y | C. | 5x2-2x2=3 | D. | 2xy-2yx=0 |
18.下列命题的逆命题是假命题的是( )
| A. | 两直线平行,同位角相等 | B. | 全等三角形的对应边相等 | ||
| C. | 直角三角形的两锐角互余 | D. | 对顶角相等 |
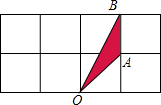 如图为正方形网格,每个小正方形的边长均为1,将△OAB绕点O逆时针旋转90°.
如图为正方形网格,每个小正方形的边长均为1,将△OAB绕点O逆时针旋转90°. 已知:矩形ABCD内有定点M.试证:AM2+CM2=BM2+DM2.
已知:矩形ABCD内有定点M.试证:AM2+CM2=BM2+DM2.