题目内容
3.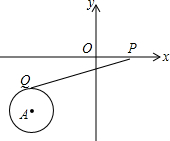 如图,点A的坐标为(-3,-2),⊙A的半径为1,P为x轴上一动点,PQ切⊙A于点Q,则当PQ最小值时,点P的坐标为( )
如图,点A的坐标为(-3,-2),⊙A的半径为1,P为x轴上一动点,PQ切⊙A于点Q,则当PQ最小值时,点P的坐标为( )| A. | (-4,0) | B. | (-2,0) | C. | (-4,0)或(-2,0) | D. | (-3,0) |
分析 连结AQ、AP,由切线的性质可知AQ⊥QP,由勾股定理可知QP=$\sqrt{A{P}^{2}-A{Q}^{2}}$,故此当AP有最小值时,PQ最短,根据垂线段最短可得到点P的坐标.
解答 解:连接AQ,AP.
根据切线的性质定理,得AQ⊥PQ;
要使PQ最小,只需AP最小,
根据垂线段最短,可知当AP⊥x轴时,AP最短,
∴P点的坐标是(-3,0).
故选:D.
点评 本题考查了切线的性质,坐标与图形性质.此题应先将问题进行转化,再根据垂线段最短的性质进行分析.

练习册系列答案
 培优口算题卡系列答案
培优口算题卡系列答案 开心口算题卡系列答案
开心口算题卡系列答案 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案
相关题目
14.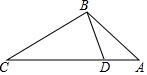 如图,点D在△ABC的边AC上,要判定△ADB与△ABC相似,添加一个条件,不正确的是( )
如图,点D在△ABC的边AC上,要判定△ADB与△ABC相似,添加一个条件,不正确的是( )
 如图,点D在△ABC的边AC上,要判定△ADB与△ABC相似,添加一个条件,不正确的是( )
如图,点D在△ABC的边AC上,要判定△ADB与△ABC相似,添加一个条件,不正确的是( )| A. | ∠ABD=∠C | B. | ∠ADB=∠ABC | C. | $\frac{AB}{BD}=\frac{CB}{CA}$ | D. | $\frac{AB}{AD}=\frac{AC}{AB}$ |
12.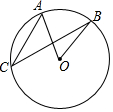 如图,⊙O中,弦AC与BC时两条弦,∠C=35°,则∠O的度数是( )
如图,⊙O中,弦AC与BC时两条弦,∠C=35°,则∠O的度数是( )
 如图,⊙O中,弦AC与BC时两条弦,∠C=35°,则∠O的度数是( )
如图,⊙O中,弦AC与BC时两条弦,∠C=35°,则∠O的度数是( )| A. | 25° | B. | 35° | C. | 65° | D. | 70° |
13.已知x是整数,并且-3<x<2,在数轴上表示x可能取的所有数值的个数为( )
| A. | 4个 | B. | 3个 | C. | 2个 | D. | 1个 |
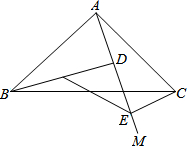 如图,在△ABC中,∠BAC=90°,AB=AC,AM是过点A的任意一条直线,BD⊥AM于点D,CE⊥AM于点E,求证:DE=BD-CE.
如图,在△ABC中,∠BAC=90°,AB=AC,AM是过点A的任意一条直线,BD⊥AM于点D,CE⊥AM于点E,求证:DE=BD-CE. 如图,直线AB,CD相交于O,OE平分∠AOD,∠FOC=100°,∠1=40°,求∠2和∠3的度数.
如图,直线AB,CD相交于O,OE平分∠AOD,∠FOC=100°,∠1=40°,求∠2和∠3的度数.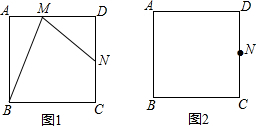
 如图,在Rt△ABC中,∠C=90°,AD平分∠CAB,DE⊥AB于E,AC=3,BC=4.
如图,在Rt△ABC中,∠C=90°,AD平分∠CAB,DE⊥AB于E,AC=3,BC=4.