题目内容
下列方程的变形中,正确的是( )
A. 方程 3x﹣2=2x+1,移项,得 3x﹣2x=﹣1+2
B. 方程 3﹣x=2﹣5(x﹣1),去括号,得 3﹣x=2﹣5x﹣1
C. 方程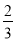 x=
x=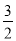 ,未知数系数化为 1,得 x=1
,未知数系数化为 1,得 x=1
D. 方程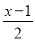 ﹣
﹣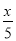 =1 化成 5(x﹣1)﹣2x=10
=1 化成 5(x﹣1)﹣2x=10
练习册系列答案
相关题目
题目内容
下列方程的变形中,正确的是( )
A. 方程 3x﹣2=2x+1,移项,得 3x﹣2x=﹣1+2
B. 方程 3﹣x=2﹣5(x﹣1),去括号,得 3﹣x=2﹣5x﹣1
C. 方程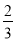 x=
x=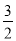 ,未知数系数化为 1,得 x=1
,未知数系数化为 1,得 x=1
D. 方程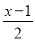 ﹣
﹣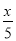 =1 化成 5(x﹣1)﹣2x=10
=1 化成 5(x﹣1)﹣2x=10