题目内容
11.已知y=$\sqrt{2x-3}$+$\sqrt{3-2x}$+5,求x+y+$\frac{5}{2}$的平方根.分析 根据被开方数大于等于0列式求出x的值,再求出y,然后代入代数式求解,再根据平方根的定义解答.
解答 解:由题意得,$\left\{\begin{array}{l}{2x-3≥0}\\{3-2x≥0}\end{array}\right.$,
解得x=$\frac{3}{2}$,
则y=5,
x+y+$\frac{5}{2}$=$\frac{3}{2}$+5+$\frac{5}{2}$=9,
所以,x+y+$\frac{5}{2}$的平方根为±3.
点评 本题考查了二次根式有意义的条件,二次根式中的被开方数必须是非负数,否则二次根式无意义.

练习册系列答案
相关题目
2.把多项式x3-4x分解因式,结果正确的是( )
| A. | x(x+2)(x-2) | B. | x(x+4)(x-4) | C. | x(x-2)2 | D. | x (x2-4) |
19.某超市四月份的营业额为30万元,第二季度的营业额为120万元,如果设平均每月的增长率为x,下列方程正确的是( )
| A. | 30(1+x)2=120 | B. | 30+30×2x=120 | ||
| C. | 30(1+x%)2=120 | D. | 30+30(1+x)+30(1+x)2=120 |
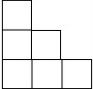
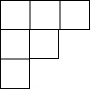
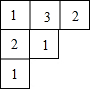 如图,是由若干个大小相同的正方体搭成的几何体的俯视图,其中小正方形中的数字表示该位置上的正方体的个数,则这个几何体的左视图是( )
如图,是由若干个大小相同的正方体搭成的几何体的俯视图,其中小正方形中的数字表示该位置上的正方体的个数,则这个几何体的左视图是( )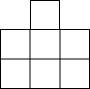

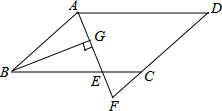 如图,在?ABCD中,AB=6,AD=9,∠BAD的平分线交BC于点E,交DC的延长线于点F,BG⊥AE,垂足为G.若BG=$4\sqrt{2}$,则△CEF的面积是2$\sqrt{2}$.
如图,在?ABCD中,AB=6,AD=9,∠BAD的平分线交BC于点E,交DC的延长线于点F,BG⊥AE,垂足为G.若BG=$4\sqrt{2}$,则△CEF的面积是2$\sqrt{2}$. 如图,是一只圆柱形的封闭易拉罐,它的底面半径为4cm,高为15cm,问易拉罐内可放的搅拌棒(直线型)最长是多长?
如图,是一只圆柱形的封闭易拉罐,它的底面半径为4cm,高为15cm,问易拉罐内可放的搅拌棒(直线型)最长是多长?