题目内容
16.先阅读第(1)题的解法,再解答其他各题.(1)已知y=$\sqrt{2013-x}$+$\sqrt{x-2013}$+2014,求$\frac{y}{x}$的值.
解:由$\left\{\begin{array}{l}{2013-x≥0}\\{x-2013≥0}\end{array}\right.$,得x=2013,∴y2014,
∴$\frac{y}{x}$=$\frac{2014}{2013}$.
(2)若x、y为实数,其y>$\sqrt{x-3}$+$\sqrt{3-x}$+2,化简$\frac{|1-y|}{y-1}$;
(3)如果$\sqrt{2x-y-4}$+$\sqrt{x-2y-5}$=0,求$\sqrt{{y}^{2}+5x}$的值.
分析 (2)根据被开方数大于等于0列式求出x,再求出y的取值范围,然后化简即可;
(3)根据非负数的性质列出方程组,然后求出x、y,再代入代数式进行计算即可得解.
解答 解:(2)由$\left\{\begin{array}{l}{x-3≥0}\\{3-x≥0}\end{array}\right.$得x=3,
所以y>2,
所以$\frac{|1-y|}{y-1}$=$\frac{y-1}{y-1}$=1;
(3)由题意得,$\left\{\begin{array}{l}{2x-y-4=0}\\{x-2y-5=0}\end{array}\right.$,
解得$\left\{\begin{array}{l}{x=1}\\{y=-2}\end{array}\right.$.
所以,$\sqrt{{y}^{2}+5x}$=$\sqrt{(-2)^{2}+5×1}$=3.
点评 本题考查的知识点为:分式有意义,分母不为0;二次根式的被开方数是非负数,读懂题目信息,理解求解方法是解题的关键.

练习册系列答案
相关题目
4.一元二次方程x2=2x的根是( )
| A. | 0 | B. | 2 | C. | 0和2 | D. | 0和-2 |
6.(x2+x+5)(x2+x-6)变形正确的是( )
| A. | (x2+x)2+(x2+x)-30 | B. | (x2+x)2+(x2+x)-30 | C. | (x2+x)2+5(x2+x)-30 | D. | (x2+x)2-(x2+x)-30 |
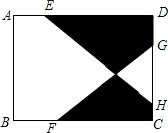 如图,在矩形ABCD中,点E、F分别在边AD、BC上,点G、H在DC边上,且AE:AD=1:4,BF:BC=1:4,GH=$\frac{1}{2}$DC,AB=10,BC=12,则图中阴影部分面积为52.5.
如图,在矩形ABCD中,点E、F分别在边AD、BC上,点G、H在DC边上,且AE:AD=1:4,BF:BC=1:4,GH=$\frac{1}{2}$DC,AB=10,BC=12,则图中阴影部分面积为52.5. 为参加成都市“体考”,某中学将某班50名同学一周的体育锻炼情况绘制成了如图所示的条形统计图,根据统计图提供的数据,该班50名同学一周参加体育锻炼时间的中位数与众数之和为17 小时.
为参加成都市“体考”,某中学将某班50名同学一周的体育锻炼情况绘制成了如图所示的条形统计图,根据统计图提供的数据,该班50名同学一周参加体育锻炼时间的中位数与众数之和为17 小时.