题目内容
已知a、b是正实数,那么, 是恒成立的.
是恒成立的.
(1)由 恒成立,说明
恒成立,说明 恒成立;
恒成立;
(2)填空:已知a、b、c是正实数,由 恒成立,猜测:
恒成立,猜测: ( )也恒成立。
( )也恒成立。
(3)如图,已知AB是直径,点P是弧上异于点A和点B的一点,PC⊥AB,垂足为C,AC=a,BC=b,由此图说明 恒成立.
恒成立.
 是恒成立的.
是恒成立的.(1)由
 恒成立,说明
恒成立,说明 恒成立;
恒成立;(2)填空:已知a、b、c是正实数,由
 恒成立,猜测:
恒成立,猜测: ( )也恒成立。
( )也恒成立。(3)如图,已知AB是直径,点P是弧上异于点A和点B的一点,PC⊥AB,垂足为C,AC=a,BC=b,由此图说明
 恒成立.
恒成立.
解:(1)∵( ﹣
﹣ )2≥0,
)2≥0,
a﹣2 +b≥0
+b≥0
a+b≥2
 ≥
≥
(2)
(3)如图,连接OP,∵AB是直径,∴∠APB=90°,
又∵PC⊥AB,∴∠ACP=∠ACB=90°,
∴∠A+∠B=∠A+∠APC=90°,∴∠APC=∠B,
∴Rt△APC∽Rt△PBC,
∴ ,∴PC2=AC×CB=ab,
,∴PC2=AC×CB=ab,
∴PC= ,又∵PO=
,又∵PO= ,
,
∵PO≥PC,∴ .
.
 ﹣
﹣ )2≥0,
)2≥0,a﹣2
 +b≥0
+b≥0a+b≥2

 ≥
≥
(2)

(3)如图,连接OP,∵AB是直径,∴∠APB=90°,
又∵PC⊥AB,∴∠ACP=∠ACB=90°,
∴∠A+∠B=∠A+∠APC=90°,∴∠APC=∠B,
∴Rt△APC∽Rt△PBC,
∴
 ,∴PC2=AC×CB=ab,
,∴PC2=AC×CB=ab,∴PC=
 ,又∵PO=
,又∵PO= ,
,∵PO≥PC,∴
 .
.
练习册系列答案
相关题目
 (2012•资阳)已知a、b是正实数,那么,
(2012•资阳)已知a、b是正实数,那么, 已知a,b是正实数,
已知a,b是正实数,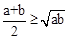 是恒成立的.
是恒成立的.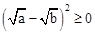 恒成立,说明
恒成立,说明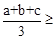 ▲ 也恒成立;
▲ 也恒成立;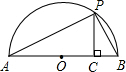
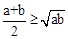 是恒成立的.
是恒成立的. 恒成立,说明
恒成立,说明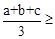 ▲ 也恒成立;
▲ 也恒成立;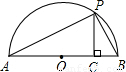
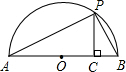 已知a、b是正实数,那么,
已知a、b是正实数,那么, 是恒成立的.
是恒成立的.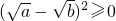 恒成立,说明
恒成立,说明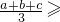 ______也恒成立;
______也恒成立;