题目内容
已知a、b是正实数,那么,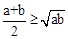 是恒成立的.
是恒成立的.
(1)(3分)由 恒成立,说明
恒成立,说明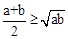 恒成立;
恒成立;
(2)(3分)填空:已知a、b、c是正实数,由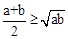 恒成立,猜测:
恒成立,猜测: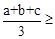 ▲ 也恒成立;
▲ 也恒成立;
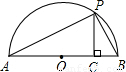
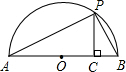
(3)(2分)如图,已知AB是直径,点P是弧上异于点A和点B的一点,PC⊥AB,垂足为C,AC=a,BC=b,由此图说明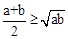 恒成立.
恒成立.
【答案】
(1)见解析(2) (3)见解析
(3)见解析
【解析】解:(1)由 得,
得, 。
。
∴于是  ,即
,即 。
。
(2) 。
。
(3)连接OP。
∵AB是直径,∴∠APB=90°。
又∵PC⊥AB,∴Rt△APC∽Rt△PBC。
∴ ,即
,即 ,∴
,∴ 。
。
又∵PO= ,由垂线段最短,得PO≥PC,即
,由垂线段最短,得PO≥PC,即 。
。
(1)由 ,利用完全平方公式,即可证得
,利用完全平方公式,即可证得 恒成立。
恒成立。
(2)设x≥0,y≥0,z≥0,
∵ ,
,
∴ ,即
,即 。
。
令 ,得
,得 。
。
(3)首先证得Rt△APC∽Rt△PBC,由相似三角形的对应边成比例,可求得PC的值,又由OP是半径,可求得OP= ,然后由点到线的距离垂线段最短,即可证得
,然后由点到线的距离垂线段最短,即可证得 恒成立。
恒成立。

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 (2012•资阳)已知a、b是正实数,那么,
(2012•资阳)已知a、b是正实数,那么, 已知a,b是正实数,
已知a,b是正实数,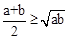 是恒成立的.
是恒成立的.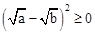 恒成立,说明
恒成立,说明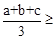 ▲ 也恒成立;
▲ 也恒成立;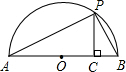
 已知a、b是正实数,那么,
已知a、b是正实数,那么, 是恒成立的.
是恒成立的.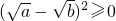 恒成立,说明
恒成立,说明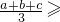 ______也恒成立;
______也恒成立;