题目内容
9.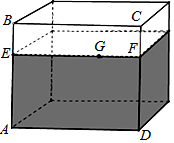 有一个如图所示的长方体透明玻璃鱼缸,假设其长AD=80cm,高AB=60cm,水深AE=40cm,在水面上紧贴内壁G处有一块面包屑,G在水面线EF上,且EG=60cm,一只蚂蚁想从鱼缸外的A点沿鱼缸壁爬进鱼缸内的G处面包屑.
有一个如图所示的长方体透明玻璃鱼缸,假设其长AD=80cm,高AB=60cm,水深AE=40cm,在水面上紧贴内壁G处有一块面包屑,G在水面线EF上,且EG=60cm,一只蚂蚁想从鱼缸外的A点沿鱼缸壁爬进鱼缸内的G处面包屑.(1)该蚂蚁应该沿怎样的路线爬行才能使路程最短呢?请你画出它爬行的路线,并用箭头标注;
(2)求蚂蚁爬行的最短路线长.
分析 (1)做出A关于BC的对称点A′,连接A′G,与BC交于点Q,此时AQ+QG最短;
(2)A′G为直角△A′EG的斜边,根据勾股定理求解即可.
解答 解:(1)如图所示作点A关于BC的对称点A′,连接A′G交BC与点Q,蚂蚁沿着A→Q→G的路线爬行时,路程最短.
(2)∵在直角△A′EG中,A′E=80cm,EG=60cm,
∴AQ+QG=A′Q+QG=A′G=$\sqrt{A′{E}^{2}+E{G}^{2}}$=100cm.
∴最短路线长为100cm.
点评 本题考查最短路径问题,关键知道两点之间线段最短,从而可找到路径求出解.

练习册系列答案
相关题目
14.下列数中是无理数的是( )
| A. | $\frac{22}{7}$ | B. | $\sqrt{81}$ | C. | π-3.14 | D. | $\sqrt{2}$ |
18.化简$\frac{3}{\sqrt{6}}$的结果是( )
| A. | 2 | B. | $\frac{1}{2}$ | C. | $\frac{1}{2}$$\sqrt{6}$ | D. | 以上答案都不对 |
19.下列各命题的逆命题成立的是( )
| A. | 对顶角相等 | B. | 如果a=b,那么|a|=|b| | ||
| C. | 全等三角形的对应角相等 | D. | 两直线平行,同位角相等 |
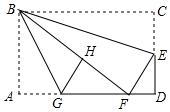 如图,在矩形纸片ABCD中,AB=6,BC=10,点E在CD上,将△BCE沿BE折叠,点C恰落在边AD上的点F处;点G在AF上,将△ABG沿BG折叠,点A恰落在线段BF上的点H处,有下列结论:
如图,在矩形纸片ABCD中,AB=6,BC=10,点E在CD上,将△BCE沿BE折叠,点C恰落在边AD上的点F处;点G在AF上,将△ABG沿BG折叠,点A恰落在线段BF上的点H处,有下列结论: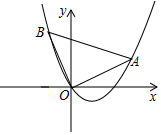 如图,在平面直角坐标系中,O为坐标原点,△AOB是等腰直角三角形,∠AOB=90°,A(2,1).
如图,在平面直角坐标系中,O为坐标原点,△AOB是等腰直角三角形,∠AOB=90°,A(2,1).