题目内容
1.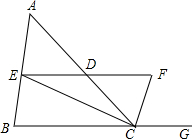 如图,CE,CF分别平分∠ACB和∠ACB的外角,EF∥BC交AC于D.
如图,CE,CF分别平分∠ACB和∠ACB的外角,EF∥BC交AC于D.(1)∠ECF=90°.
(2)试说明:DE=DF.
(3)当∠ACB=90°时,△CEF为等腰三角形.
分析 (1)根据角平分线的定义得到∠ACE=$\frac{1}{2}$∠ACB,∠ACF=$\frac{1}{2}$∠ACG,则∠ACE+∠ACF=$\frac{1}{2}$(∠ACB+∠ACG),然后根据平角的定义即可得到∠ACE+∠ACF=90°;
(2)利用平行线及角平分线的性质先求得CD=ED,CD=DF,然后等量代换即可证明DE=DF;
(3)在Rt△CEF中,CF=EF,求得∠FEC=45°,根据平行线的性质得到∠BBCE=45°,求得∠ACB=2∠ECB=90°,即可得到结论.
解答 解:(1)∵CE、CF分别平分∠ACB和△ABC的外角∠ACG,
∴∠ACE=$\frac{1}{2}$∠ACB,∠ACF=$\frac{1}{2}$∠ACG,
∴∠ACE+∠ACF=$\frac{1}{2}$(∠ACB+∠ACG),
而∠ACB+∠ACG=180°,
∴∠ACE+∠ACF=$\frac{1}{2}$×180°=90°,
即∠ECF=90°;
故答案为:90°;
(2)∵CE是△ABC的角平分线,
∴∠ACE=∠BCE.
∵CF为外角∠ACG的平分线,
∴∠ACF=∠GCF.
∵EF∥BC,
∴∠GCF=∠F,∠BCE=∠CEF.
∴∠ACE=∠CEF,∠F=∠DCF.
∴CD=ED,CD=DF(等角对等边).
∴DE=DF
(3)当∠ACB=90°时,△CEF为等腰三角形.
在Rt△CEF中,CF=EF,
∴∠FEC=45°,
∴∠BBCE=45°,
∴∠ACB=2∠ECB=90°,
即∠ACB=90°时,△CEF为等腰三角形.
故答案为:90°.
点评 本题考查了等腰三角形的判定及角平分线的性质和平行线的性质;进行等量代换是正确解答本题的关键.

练习册系列答案
相关题目
12.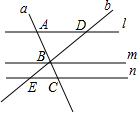 如图,已知直线l∥m∥n,直线a分别与l,m,n交于点A,B,C,过点B作直线b交直线l,n于点D,E,若AB=2,BC=1,BD=3,则BE的长为( )
如图,已知直线l∥m∥n,直线a分别与l,m,n交于点A,B,C,过点B作直线b交直线l,n于点D,E,若AB=2,BC=1,BD=3,则BE的长为( )
 如图,已知直线l∥m∥n,直线a分别与l,m,n交于点A,B,C,过点B作直线b交直线l,n于点D,E,若AB=2,BC=1,BD=3,则BE的长为( )
如图,已知直线l∥m∥n,直线a分别与l,m,n交于点A,B,C,过点B作直线b交直线l,n于点D,E,若AB=2,BC=1,BD=3,则BE的长为( )| A. | 4 | B. | 2 | C. | $\frac{2}{3}$ | D. | $\frac{3}{2}$ |
16. 如图,在△ABC中,∠C=90°,∠B=30°,以A为圆心,任意长为半径画弧分别交AB、AC于点M和N,再分别以M、N为圆心,大于MN的长为半径画弧,两弧交于点P,连接AP并延长交BC于点D,则下列说法不正确的是( )
如图,在△ABC中,∠C=90°,∠B=30°,以A为圆心,任意长为半径画弧分别交AB、AC于点M和N,再分别以M、N为圆心,大于MN的长为半径画弧,两弧交于点P,连接AP并延长交BC于点D,则下列说法不正确的是( )
 如图,在△ABC中,∠C=90°,∠B=30°,以A为圆心,任意长为半径画弧分别交AB、AC于点M和N,再分别以M、N为圆心,大于MN的长为半径画弧,两弧交于点P,连接AP并延长交BC于点D,则下列说法不正确的是( )
如图,在△ABC中,∠C=90°,∠B=30°,以A为圆心,任意长为半径画弧分别交AB、AC于点M和N,再分别以M、N为圆心,大于MN的长为半径画弧,两弧交于点P,连接AP并延长交BC于点D,则下列说法不正确的是( )| A. | AD是∠BAC的平分线 | B. | ∠ADC=60° | ||
| C. | 点D是AB的垂直平分线上 | D. | 如果CD=2,AB=7,则可得S△ABD=14 |
6. 有理数a和b在数轴上的位置如图所示,则下列关系正确的是( )
有理数a和b在数轴上的位置如图所示,则下列关系正确的是( )
 有理数a和b在数轴上的位置如图所示,则下列关系正确的是( )
有理数a和b在数轴上的位置如图所示,则下列关系正确的是( )| A. | a+b<0 | B. | ab>0 | C. | -a<b<0 | D. | -a<-b<0 |
10.下列分解因式结果正确的是( )
| A. | y3-y=y(y2-1) | B. | x2-x-3=x(x-1)-3 | C. | -m2+n2=-(m-n)(m+n) | D. | x2-3x+9=(x-3)2 |
11.如图,经过折叠能围成一个正方体的是( )
| A. |  | B. |  | C. |  | D. |  |
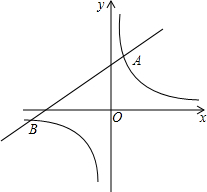 如图,已知反比例函数y=$\frac{m}{x}$的图象与一次函数y=2x+b的图象相交于点A(1,4)和点B(n,-2).
如图,已知反比例函数y=$\frac{m}{x}$的图象与一次函数y=2x+b的图象相交于点A(1,4)和点B(n,-2).