题目内容
 如图,直线L与⊙O相交于A、B两点,且与半径OC垂直,垂足为H,已知AB=16cm,HB:OB=4:5.
如图,直线L与⊙O相交于A、B两点,且与半径OC垂直,垂足为H,已知AB=16cm,HB:OB=4:5.(1)求⊙O的半径;
(2)如果要将直线L平移到与⊙O相切的位置,平移的距离应是多少?请说明理由.
考点:切线的性质,勾股定理,垂径定理,平移的性质
专题:计算题
分析:(1)根据垂径定理得AH=BH=
AB=8,则由HB:OB=4:5可得OB=10;
(2)在Rt△OBH中根据勾股定理得OH=6,则CH=OC-OH=4,根据切线的性质,当直线L过点C时,直线L与⊙O相切,则向下平移4个单位;同样当直线L向上平移16个单位时,直线L与⊙O相切.
| 1 |
| 2 |
(2)在Rt△OBH中根据勾股定理得OH=6,则CH=OC-OH=4,根据切线的性质,当直线L过点C时,直线L与⊙O相切,则向下平移4个单位;同样当直线L向上平移16个单位时,直线L与⊙O相切.
解答:解:(1)∵AB⊥OC,
∴AH=BH=
AB=
×16=8,
∵HB:OB=4:5,
∴OB=10,
即⊙O的半径为10;
(2)将直线L平移到与⊙O相切的位置,平移的距离是4个单位或16个单位.理由如下:
在Rt△OBH中,∵BH=8,OB=10,
∴OH=
=6,
∴CH=OC-OH=10-6=4,
∴当直线L过点C时,直线L与⊙O相切,此时向下平移4个单位;
同样当直线L向上平移16个单位时,直线L与⊙O相切.
∴AH=BH=
| 1 |
| 2 |
| 1 |
| 2 |
∵HB:OB=4:5,
∴OB=10,
即⊙O的半径为10;
(2)将直线L平移到与⊙O相切的位置,平移的距离是4个单位或16个单位.理由如下:
在Rt△OBH中,∵BH=8,OB=10,
∴OH=
| OB2-BH2 |
∴CH=OC-OH=10-6=4,
∴当直线L过点C时,直线L与⊙O相切,此时向下平移4个单位;
同样当直线L向上平移16个单位时,直线L与⊙O相切.
点评:本题考查了切线的性质:圆的切线垂直于经过切点的半径.也考查了勾股定理与垂径定理.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
若|a|=8,|b|=7,且a+b>0,那么a-b的值为( )
| A、1或15 |
| B、-1或-15 |
| C、1或-1 |
| D、15或-15 |
如果由四舍五入得到的近似数75,那原数不可能是( )
| A、74.48 |
| B、74.53 |
| C、74.87 |
| D、75.49 |
 如图,在方格纸上建立的平面直角坐标系中,作△ABO关于y轴的对称图形,得到△A′B′O.求点A′的坐标及△OBB′的面积.
如图,在方格纸上建立的平面直角坐标系中,作△ABO关于y轴的对称图形,得到△A′B′O.求点A′的坐标及△OBB′的面积.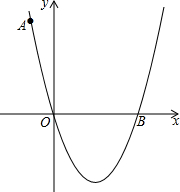 如图,在平面直角坐标系中,抛物线y=ax2+bx+c经过O(0,0),A(-1,5),B(4,0)三点,请在该抛物线对称轴上作一点P,使得AP+OP的值最小,并求出最小值.(请用尺规作图完成,不写作法,但保留作图痕迹)
如图,在平面直角坐标系中,抛物线y=ax2+bx+c经过O(0,0),A(-1,5),B(4,0)三点,请在该抛物线对称轴上作一点P,使得AP+OP的值最小,并求出最小值.(请用尺规作图完成,不写作法,但保留作图痕迹)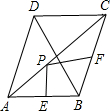 如图,菱形ABCD中,对角线AC=8,BD=6,点E,F分别是边AB,BC的中点,点P在AC上运动,在运动过程中,存在PE+PF的最小值,则这个最小值是( )
如图,菱形ABCD中,对角线AC=8,BD=6,点E,F分别是边AB,BC的中点,点P在AC上运动,在运动过程中,存在PE+PF的最小值,则这个最小值是( )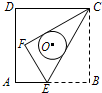 如图,正方形ABCD的边长为6,点E是AB上的一点,将△BCE沿CE折叠至△FCE,若CF,CE恰好与以正方形ABCD的中心为圆心的⊙O相切,则折痕CE的长为( )
如图,正方形ABCD的边长为6,点E是AB上的一点,将△BCE沿CE折叠至△FCE,若CF,CE恰好与以正方形ABCD的中心为圆心的⊙O相切,则折痕CE的长为( )