题目内容
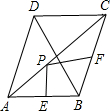 如图,菱形ABCD中,对角线AC=8,BD=6,点E,F分别是边AB,BC的中点,点P在AC上运动,在运动过程中,存在PE+PF的最小值,则这个最小值是( )
如图,菱形ABCD中,对角线AC=8,BD=6,点E,F分别是边AB,BC的中点,点P在AC上运动,在运动过程中,存在PE+PF的最小值,则这个最小值是( )| A、3 | B、4 | C、5 | D、6 |
考点:轴对称-最短路线问题,菱形的性质
专题:
分析:根据菱形的对角线互相垂直平分可得AC⊥BD,AO=
AC,BO=
BD,利用勾股定理列式求出AB,作点E关于AC的对称点E′,根据轴对称确定最短路线问题,连接E′F与AC的交点即为所求的PE+PF最小值的点P,再根据菱形的轴对称性可知E′为AD的中点,E′F的长等于菱形的边长,从而得解.
| 1 |
| 2 |
| 1 |
| 2 |
解答: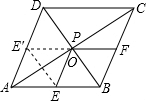 解:如图,∵四边形ABCD是菱形,
解:如图,∵四边形ABCD是菱形,
∴AC⊥BD,AO=
AC=
×8=4,BO=
BD=
×6=3,
∴AB2=32+42=25,
∴AB=5,
作点E关于AC的对称点E′,
连接E′F与AC的交点即为所求的PE+PF最小值的点P,PE+PF=E′F,
由菱形的轴对称性可知E′为AD的中点,
所以,E′F=AB=5,
即PE+PF的最小值为5.
故选:C.
 解:如图,∵四边形ABCD是菱形,
解:如图,∵四边形ABCD是菱形,∴AC⊥BD,AO=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∴AB2=32+42=25,
∴AB=5,
作点E关于AC的对称点E′,
连接E′F与AC的交点即为所求的PE+PF最小值的点P,PE+PF=E′F,
由菱形的轴对称性可知E′为AD的中点,
所以,E′F=AB=5,
即PE+PF的最小值为5.
故选:C.
点评:本题考查了轴对称确定最短路线问题,菱形的性质,勾股定理.熟练掌握菱形的性质以及最短路线的确定方法是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
已知一元二次方程2x2+x-5=0的两根分别是x1,x2,则x1+x2的值是( )
A、
| ||
B、-
| ||
C、-
| ||
D、
|
有下列说法:①有理数与数轴上的点一一对应;②直角三角形的两边长是5和12,则第三边长是13;③近似数1.5万精确到十分位;④无理数是无限小数.其中错误说法的个数有( )
| A、4个 | B、3个 | C、2个 | D、1个 |
 如图,直线L与⊙O相交于A、B两点,且与半径OC垂直,垂足为H,已知AB=16cm,HB:OB=4:5.
如图,直线L与⊙O相交于A、B两点,且与半径OC垂直,垂足为H,已知AB=16cm,HB:OB=4:5. 如图,直线l表示草原的一条河,小明家为A处,小红家为B处,小明从家去发到小红家取钓鱼工具再去河边钓鱼,问小明按怎样的路线使总路程最短?请画出这条路线.
如图,直线l表示草原的一条河,小明家为A处,小红家为B处,小明从家去发到小红家取钓鱼工具再去河边钓鱼,问小明按怎样的路线使总路程最短?请画出这条路线. 如图,已知线段a,b,c,画一条线段,使它等于a+b-c.
如图,已知线段a,b,c,画一条线段,使它等于a+b-c.