��Ŀ����
��֪x1��x2�ǹ���x��һԪ���η���x2��2(m��1)x��m2��5��0����ʵ����
(1)��(x1��1)(x2��1)��28����m��ֵ��
(2)��֪������ABC��һ�߳�Ϊ7����x1��x2ǡ���ǡ�ABC�������ߵı߳�������������ε��ܳ���
���𰸡���1��m��ֵΪ6;��2��17.
�����������������
��1�����������ϵ���Ĺ�ϵ�ɵã�x1��x2��2(m��1)��x1x2��m2��5����(x1��1)(x2��1)��28���ɵã�x1x2��(x1��x2)��27���Ӷ��õ���m2��5��2(m��1)��27���ⷽ�����m��ֵ�����ɡ�һԪ���η��̸����б�ʽ�����м��鼴�ɵõ�m��ֵ��
��2���ٵ�7Ϊ����ʱ���̵���������һ��Ϊ7�����뷽�̿ɽ��m��ֵ����ʱm��ȡֵ����������б�ʽ��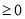 ������m��ֵ����ԭ���̣��������������ʱ������7����������������֮��Ĺ�ϵ�����Ӷ�����õ��������ε��ܳ���
������m��ֵ����ԭ���̣��������������ʱ������7����������������֮��Ĺ�ϵ�����Ӷ�����õ��������ε��ܳ���
�ڵ�7Ϊ�ױ�ʱ���̵�������ȣ��ɴ˿ɵá������б�ʽ��=0�����Ӷ��ɵù���m�ķ��̣��ⷽ�����m��ֵ������ԭ���̿���÷��̵���������������������֮��Ĺ�ϵ���鼴��.
���������
(1)(x1��1)(x2��1)��28����x1x2��(x1��x2)��27����x1��x2��2(m��1)��x1x2��m2��5��
��m2��5��2(m��1)��27��
���m1��6��m2����4��
�֦���[��2(m��1)]2��4��1��(m2��5)��0ʱ��m��2��
��m��ֵΪ6;��
(2) ��7Ϊ��������x2��2(m��1)x��m2��5��0��һ��Ϊ7��
��72��2��7��(m��1)��m2��5��0��
���m1��10��m2��4��
��m��10ʱ������x2��22x��105��0����Ϊx1��15��x2��7�����������⣬��ȥ��
��m��4ʱ������Ϊx2��10x��21��0����Ϊx1��3��x2��7����ʱ�ܳ�Ϊ7��7��3��17��
��7Ϊ�ױߣ���x2��2(m��1)x��m2��5��0�����ȸ���
�ত��0�����m��2����ʱ����Ϊx2��6x��9��0����Ϊx1��3��x2��3��3��3<7����������
�����������������ܳ�Ϊ17
�㾦����1��һԪ���η��̸���ϵ���Ĺ�ϵ������ǰ�������Ƿ���Ҫ��ʵ���������������б�ʽ��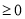 ������2���漰�����α߳��������У���õĽ������Ҫ�á�����������֮��Ĺ�ϵ�����飬�������߶��ܷ�Χ��������.
������2���漰�����α߳��������У���õĽ������Ҫ�á�����������֮��Ĺ�ϵ�����飬�������߶��ܷ�Χ��������.
�����͡������
��������
21
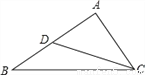
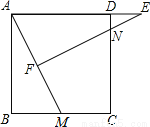
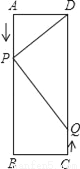
��ͼ����֪�ڡ�ABC�У�D��AB���е㣬�ҡ�ACD=��B���� AB=10����AC�ij���
 ����ѧ��Ӧ�����ϵ�д�
����ѧ��Ӧ�����ϵ�д�

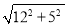 =13��AD=12��
=13��AD=12��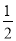 AM=6.5��
AM=6.5��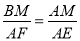 ��
��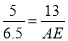 ��
��

 B.
B. 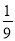 C.
C. 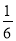 D.
D. 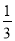
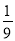 .
.