题目内容
11.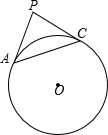 如图,已知⊙O的半径是4,AC是⊙0的弦,AP是⊙0的切线,AC=4$\sqrt{2}$,AP=4,连接PC,判断直线PC和⊙0的位置关系,并说明理由.
如图,已知⊙O的半径是4,AC是⊙0的弦,AP是⊙0的切线,AC=4$\sqrt{2}$,AP=4,连接PC,判断直线PC和⊙0的位置关系,并说明理由.
分析 连接OA,OC,PO,可证明△OAP≌△AOC,得出∠AOC=90°,则AP∥OC,得出四边形OAPC为平行四边形,再根据对角线相等的平行四边形为矩形,得出∠PCO=90°,则PC为⊙0切线.
解答 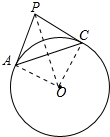 解:PC为⊙0切线,
解:PC为⊙0切线,
理由是:
连接OA,OC,PO,
∵AP是⊙0的切线,
∴∠PAO=90°,
∵AP=4,AO=4,
∴OP=4$\sqrt{2}$,
在△OAP和△AOC中,
$\left\{\begin{array}{l}{AP=OA}\\{OA=OC}\\{OP=AC}\end{array}\right.$,
∴△OAP≌△AOC,
∴∠OAP=∠AOC=90°,
∴AP∥OC,
∴四边形OAPC为平行四边形,
∵AC=OP,
∴平行四边形OAPC为矩形,
∴∠PCO=90°,
∴OC⊥PC,
∴PC为⊙0切线.
点评 本题考查了切线的判定,以及全等三角形的判定,平行四边形的判定,矩形的判定,要证某线是圆的切线,已知此线过圆上某点,连接圆心与这点(即为半径),再证垂直即可.

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案
相关题目
4.菱形有一个内角为120°,较短对角线为6,则菱形的周长为( )
| A. | 12 | B. | 24 | C. | 36 | D. | 12$\sqrt{3}$ |
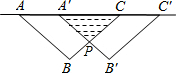 如图,把等腰Rt△ABC沿AC方向平移到等腰Rt△A′B′C′的位置时,它们重叠的部分的面积是Rt△ABC面积的$\frac{1}{4}$.若AB=$\sqrt{2}$cm,则它移动的距离AA′=1cm.
如图,把等腰Rt△ABC沿AC方向平移到等腰Rt△A′B′C′的位置时,它们重叠的部分的面积是Rt△ABC面积的$\frac{1}{4}$.若AB=$\sqrt{2}$cm,则它移动的距离AA′=1cm.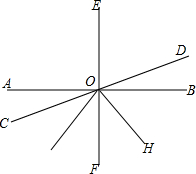 如图,AB、CD、EF相交于点O,EF⊥AB,OG平分∠COF,OH平分∠DOG,若∠AOC:∠DOH=8:29,求∠COH的大小.
如图,AB、CD、EF相交于点O,EF⊥AB,OG平分∠COF,OH平分∠DOG,若∠AOC:∠DOH=8:29,求∠COH的大小. 如图,在平面直角坐标系xOy中,点A(0,8),点B(6,8).
如图,在平面直角坐标系xOy中,点A(0,8),点B(6,8).