题目内容
16.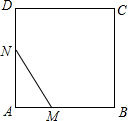 如图,已知线段AB长度是4,以AB为边作正方形ABCD,动点M,N在正方形的边上运动,且MN=3,如果点M从点A出发,沿着A→B→C→D→A的路线,向点A运动,则点M从点A运动一周回到点A的运动过程中,MN的中点P所经过的路线长度是3π+4.
如图,已知线段AB长度是4,以AB为边作正方形ABCD,动点M,N在正方形的边上运动,且MN=3,如果点M从点A出发,沿着A→B→C→D→A的路线,向点A运动,则点M从点A运动一周回到点A的运动过程中,MN的中点P所经过的路线长度是3π+4.
分析 当点M在AB上时,设点M的坐标为(m,0).由勾股定理得到点N的坐标,然后由中点坐标公式得到点P的运动轨迹的函数关系式,从而得到此时点P的运动路径是以A为圆心以$\frac{3}{2}$为半径的圆周长的$\frac{1}{4}$,当3<m≤4时,点P的轨迹为线段EF,最后可知点P运动的轨迹为3π+4.
解答 解:当点M在AB上时,设点M的坐标为(m,0).
在Rt△MNA中,AN=$\sqrt{M{N}^{2}-A{M}^{2}}$=$\sqrt{9-{m}^{2}}$,则点N的坐标为(0,$\sqrt{9-{m}^{2}}$).
由线段的中点坐标公式得:点P的坐标为($\frac{m}{2}$,$\frac{\sqrt{9-{m}^{2}}}{2}$).
∵x=$\frac{m}{2}$,y=$\frac{\sqrt{9-{m}^{2}}}{2}$,
∴${x}^{2}+{y}^{2}=\frac{9}{4}$.
∴当0≤m≤3时,点P的轨迹为以A为圆心以$\frac{3}{2}$为半径的圆周长的$\frac{1}{4}$.
当3<m≤4时,点P的轨迹为线段EF.
同理可得到点M在BC、CD、DA上运动时,点P的轨迹.
点M从点A运动一周回到点A的运动过程中,MN的中点P所经过的路线如图所示: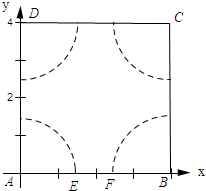
∴点P所经过的路线=($\frac{1}{4}$×2$π×\frac{3}{2}$+1)×4=3π+4.
故答案为:3π+4.
点评 本题主要考查的是点的轨迹问题,求得当0≤m≤3时,点P的运动轨迹的函数关系式是解题的关键.

练习册系列答案
相关题目
1.下列各式中不是方程的是( )
| A. | 2x=1 | B. | 2x+y=3 | C. | 7+8=15 | D. | $\frac{1}{7}$x=2 |
5.二次函数y=ax2+bx+c(a、b、c为常数,且a≠0)中的x与y的部分对应值如下表:
(1)ac<0;(2)当x>1时,y的值随x值得增大而增大;(3)-1是方程ax2+bx+c=0的一个根;(4)当-1<x<2时,ax2+bx+c<0,其中正确的个数为( )
| x | … | 0 | 1 | 2 | … |
| y | … | 4 | -4 | 6 | … |
| A. | 4个 | B. | 3个 | C. | 2个 | D. | 1个 |
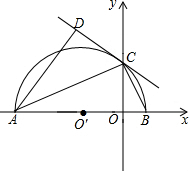 如图所示,在平面直角坐标系xOy中,AB在x轴上,以AB为直径的半⊙Oˊ与y轴正半轴交于点C,连接BC,AC.CD是半⊙Oˊ的切线,AD⊥CD于点D.
如图所示,在平面直角坐标系xOy中,AB在x轴上,以AB为直径的半⊙Oˊ与y轴正半轴交于点C,连接BC,AC.CD是半⊙Oˊ的切线,AD⊥CD于点D.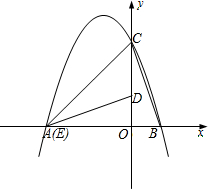 如图,二次函数y=ax2+bx+c的图象交x轴于A、B两点,交y轴于点C.且B(1,0),若将△BOC绕点O逆时针旋转90°,所得△DOE的顶点E恰好与点A重合,且△ACD的面积为3.
如图,二次函数y=ax2+bx+c的图象交x轴于A、B两点,交y轴于点C.且B(1,0),若将△BOC绕点O逆时针旋转90°,所得△DOE的顶点E恰好与点A重合,且△ACD的面积为3.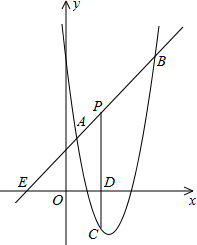 如图,直线y=x+2与抛物线y=ax2+bx+6(a≠0)相交于A($\frac{1}{2}$,$\frac{5}{2}$)和B(4,m),点P是线段AB上异于A、B的动点,过点P作PC⊥x轴于点D,交抛物线于点C.当△PAC为直角三角形时点P的坐标(3,5)或($\frac{7}{2}$,$\frac{11}{2}$).
如图,直线y=x+2与抛物线y=ax2+bx+6(a≠0)相交于A($\frac{1}{2}$,$\frac{5}{2}$)和B(4,m),点P是线段AB上异于A、B的动点,过点P作PC⊥x轴于点D,交抛物线于点C.当△PAC为直角三角形时点P的坐标(3,5)或($\frac{7}{2}$,$\frac{11}{2}$).