题目内容
1.(1)先化简,再求值:$\frac{x}{{x}^{2}-2x+1}$÷($\frac{x+1}{{x}^{2}-1}$+1),其中x=$\sqrt{2}$+1;(2)已知:x=$\frac{\sqrt{3}+\sqrt{2}}{\sqrt{3}-\sqrt{2}}$,y=$\frac{\sqrt{3}-\sqrt{2}}{\sqrt{3}+\sqrt{2}}$,求$\frac{{x}^{3}-x{y}^{2}}{{x}^{4}y+2{x}^{3}{y}^{2}+{x}^{2}{y}^{3}}$的值.
分析 (1)首先把括号内的分式通分相加,把除法转化为乘法,然后进行乘法运算即可化简,再代入数值计算即可;
(2)把所求的分式的分子和分母分解因式,然后对x和y进行化简,代入求值.
解答 解:(1)原式=$\frac{x}{(x-1)^{2}}$÷$\frac{x+1+{x}^{2}-1}{(x+1)(x-1)}$
=$\frac{x}{(x-1)^{2}}$÷$\frac{x(x+1)}{(x+1)(x-1)}$
=$\frac{x}{(x-1)^{2}}$•$\frac{(x+1)(x-1)}{x(x+1)}$
=$\frac{1}{x-1}$,
当x=$\sqrt{2}$+1时,原式=$\frac{1}{\sqrt{2}}$=$\frac{\sqrt{2}}{2}$;
(2)原式=$\frac{x(x+y)(x-y)}{{x}^{2}y(x+y)^{2}}$=$\frac{x-y}{xy(x+y)}$.
∵x=$\frac{\sqrt{3}+\sqrt{2}}{\sqrt{3}-\sqrt{2}}$=($\sqrt{3}$+$\sqrt{2}$)2=5+2$\sqrt{6}$,y=$\frac{\sqrt{3}-\sqrt{2}}{\sqrt{3}+\sqrt{2}}$=($\sqrt{3}$+$\sqrt{2}$)2=5-2$\sqrt{6}$,
∴xy=1,x+y=10,x-y=4$\sqrt{6}$.
∴原式=$\frac{4\sqrt{6}}{10}$=$\frac{2\sqrt{6}}{5}$.
点评 本题考查了分式的化简求值以及二次根式的运算,正确对分式的分子、分母进行分解因式是关键.

练习册系列答案
相关题目
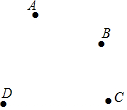 如图所示,平面上有四个点A、B、C、D,根据下列语句画图:
如图所示,平面上有四个点A、B、C、D,根据下列语句画图: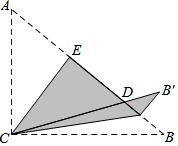 如图,Rt△ABC中,∠ACB=90°,AC=3,BC=4,将边AC沿CE翻折,使点A落在AB上的点D处;再将边BC沿CF翻折,使点B落在CD的延长线上的点B'处,两条折痕与斜边AB分别交于点E、F,则AD=$\frac{18}{5}$;B'F=$\frac{4}{5}$.
如图,Rt△ABC中,∠ACB=90°,AC=3,BC=4,将边AC沿CE翻折,使点A落在AB上的点D处;再将边BC沿CF翻折,使点B落在CD的延长线上的点B'处,两条折痕与斜边AB分别交于点E、F,则AD=$\frac{18}{5}$;B'F=$\frac{4}{5}$.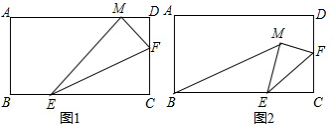
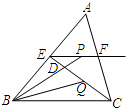 如图所示,在△ABC中,BC=4,E、F分别是AB、AC上的点,且EF∥BC,动点P在射线EF上,BP交CE于点D,∠CBP的平分线交CE于Q,当CQ=$\frac{1}{3}$CE时,EP+BP=8.
如图所示,在△ABC中,BC=4,E、F分别是AB、AC上的点,且EF∥BC,动点P在射线EF上,BP交CE于点D,∠CBP的平分线交CE于Q,当CQ=$\frac{1}{3}$CE时,EP+BP=8.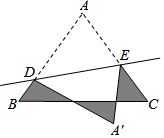 如图,等边△ABC的边长是5,D、E分别是边AB、AC上的点,将△ADE沿直线DE折叠,点A落在A′处,且点A′在△ABC外部,则阴影图形的周长为15.
如图,等边△ABC的边长是5,D、E分别是边AB、AC上的点,将△ADE沿直线DE折叠,点A落在A′处,且点A′在△ABC外部,则阴影图形的周长为15. 如图,平行四边形ABCD的周长为36,对角线AC,BD相交于点O,点E是CD的中点,BD=12,则△DOE的周长是15.
如图,平行四边形ABCD的周长为36,对角线AC,BD相交于点O,点E是CD的中点,BD=12,则△DOE的周长是15. 如图,菱形ABCD的边长为5,对角线AC=8.
如图,菱形ABCD的边长为5,对角线AC=8.