题目内容
 如图,在△ABC中,∠C=90°,sinB=
如图,在△ABC中,∠C=90°,sinB=| 3 |
| 5 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
考点:同角三角函数的关系
专题:
分析:根据sin2B+cos2B=1及∠B为锐角,可得出cosB的值.
解答:解:∵sin2B+cos2B=1,sinB=
,
∴cosB=±
,
∵∠B为锐角,
∴cosB=
.
故选D.
| 3 |
| 5 |
∴cosB=±
| 4 |
| 5 |
∵∠B为锐角,
∴cosB=
| 4 |
| 5 |
故选D.
点评:本题考查了同角的三角函数关系式,属于基础题,注意掌握sin2B+cos2B=1.

练习册系列答案
相关题目
 如图,∠AOB是平角,∠AOC,∠BOC的角平分线分别是OD,OE,则∠DOE是( )
如图,∠AOB是平角,∠AOC,∠BOC的角平分线分别是OD,OE,则∠DOE是( )| A、80° | B、90° |
| C、100° | D、105° |
若a≠0,下列等式一定成立的是( )
| A、a6÷a3=a2 |
| B、a2•a3=a6 |
| C、a2•a3=a5 |
| D、(a2)3=a5 |
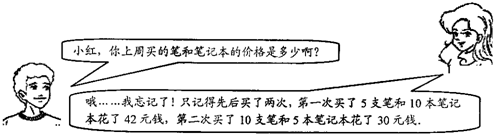
根据以下对话,可以求得小红所买的笔和笔记本的价格分别是( )

| A、0.8元/支,2.6元/本 |
| B、0.8元/支,3.6元/本 |
| C、1.2元/支,3.6元/本 |
| D、1.2元/支,2.6元/本 |
在反比例函数y=
图象的每个象限内,y随x的增大而减少,则k值可以是( )
| k-2 |
| x |
| A、3 | B、2 | C、1 | D、-1 |
 如图,在Rt△OAB中,OA=8,OB=6,点C在OA上,AC=2,⊙P的圆心P在线段BC上,且与⊙P与边AB,AO都相切.若反比例函数y=
如图,在Rt△OAB中,OA=8,OB=6,点C在OA上,AC=2,⊙P的圆心P在线段BC上,且与⊙P与边AB,AO都相切.若反比例函数y=