题目内容
在Rt△ABC中，∠C=90°，BD平分∠ABC，CD=n，AB=m，则△ABD的面积是 ．
考点：角平分线的性质
专题：计算题
分析：作出图形，过点D作DE⊥AB于E，根据角平分线上的点到角的两边距离相等可得DE=CD，然后利用三角形的面积公式列式计算即可得解．
解答：
解：如图，过点D作DE⊥AB于E，
∵∠C=90°，BD平分∠ABC，
∴DE=CD=n，
∴△ABD的面积=
AB•DE=
mn．
故答案为：
mn．
解：如图，过点D作DE⊥AB于E，∵∠C=90°，BD平分∠ABC，
∴DE=CD=n，
∴△ABD的面积=
| 1 |
| 2 |
| 1 |
| 2 |
故答案为：
| 1 |
| 2 |
点评：本题考查了角平分线上的点到角的两边距离相等的性质，熟记性质是解题的关键，作出图形更形象直观．
练习册系列答案
学而优衔接教材南京大学出版社系列答案
小学课堂作业系列答案
金博士一点全通系列答案
相关题目
如图，点P是抛物线y=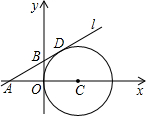
如图在平面直角坐标系中，⊙C与y轴相切，且C点坐标为（1，0），直线l过点A（-1，0），与⊙C相切于点D，求直线l的解析式．