题目内容
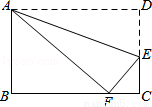
如图，将矩形ABCD沿AE折叠，点D恰好落在BC边上的点F处，如果AB：AD=2：3，那么tan∠EFC值是 ．
.
【解析】
试题分析：根据AB：AD=2：3，以及折叠的性质表示出三角形ABF的各边长，然后利用等角变换得出∠BAF=∠CFE，继而可得出答案．
试题解析：∵AB：AD=2：3，
∴在Rt△ABF中，设AB=2x，AF=AD=BC=3x，
则BF=
，
又∵∠EFC+∠AFB=90°，∠AFB+∠BAF=90°，
∴∠BAF=∠CFE，
故tan∠EFC=tan∠BAF=
．
考点：翻折变换（折叠问题）．
练习册系列答案
举一反三单元同步过关卷系列答案
相关题目
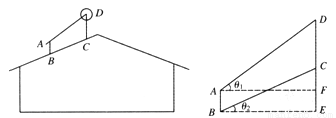
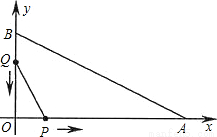
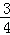，在与山脚C距离200米的D处，测得山顶A的仰角为26.6°，求小山岗的高AB（结果取整数：参考数据：sin26.6°=0.45，cos26.6°=0.89，tan26.6°=0.50）．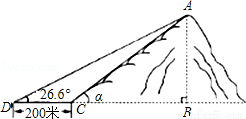
，该双曲线位于第一、三象限的概率是 ．
：
和直线
.我们约定：当x任取一值时,x对应的函数值分别为y1、y2，若y1≠y2，取y1、y2中的较小值记为M；若y1=y2，记M= y1=y2.下列判断： 