��Ŀ����
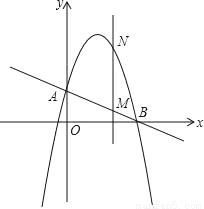
��ͼ��ֱ��AB�ֱ�y�ᡢx����A��B���㣬OA=2��tan��ABO=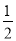 ��������y=��x2+bx+c��A��B���㣮
��������y=��x2+bx+c��A��B���㣮
��1����ֱ��AB����������ߵĽ���ʽ��
��2���������ߵĶ���ΪD�����ABD�������
��3������ֱx���ֱ��x=t���ڵ�һ����ֱ��AB��M���������������N����tȡ��ֵʱ��MN�ij���l�����ֵ�����ֵ�Ƕ��٣�
��ϰ��ϵ�д�
 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
�����Ŀ