题目内容
2.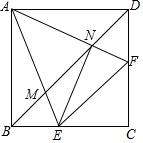 如图,四边形ABCD是正方形,点E和点F分别在BC和CD上,∠EAF=45°,AE、AF分别交BD于点M、N,连接EF,EN
如图,四边形ABCD是正方形,点E和点F分别在BC和CD上,∠EAF=45°,AE、AF分别交BD于点M、N,连接EF,EN(1)图中与△BME相似的三角形有△AMN,△DNF,△ADM,△AEF;
(2)求证:EF=$\sqrt{2}$MN;
(3)求证:△AEN是等腰直角三角形.
分析 (1)与△BME相似的三角形有△AMN,△DNF,△ADM,△AEF,△ABN.根据相似三角形的判定方法一一判断即可.
(2)首先证明△ANE是等腰直角三角形,推出AE=$\sqrt{2}$AN,再证明△AMN∽△AFE即可解决问题.
解答 (1)解:与△BME相似的三角形有△AMN,△DNF,△ADM,△AEF.
理由:∵四边形ABCD是正方形,
∴∠EBM=∠ADM=∠FDN=∠ABD=45°,
∵∠MAN=∠EBM=45°,∠AMN=∠BME,
∴△AMN∽△BME.
∴∠ANM=∠MEB,
∵∠DNF=∠ANM,
∴∠DNF=∠BEM,∵∠NDF=∠EBM=45°,
∴△DFN∽△BME.
∵∠ADM=∠EBM=45°,∠AMD=∠BME,
∴△DMA∽△BME.
将△ADF绕点A顺时针旋转90°得到△ABH,
在△AEF和△AEH中,
$\left\{\begin{array}{l}{AE=AE}\\{∠EAH=∠EAF}\\{AH=AF}\end{array}\right.$,
∴△AEF≌△AEH,
∴∠AEB=∠AEF,
∵∠EAF=∠EBM,
∴△AEF∽△BEM.
∵∠ABN=∠EBM,∠ANB=∠BEM,
∴△BEM∽△BNA,
故答案为△AMN,△DNF,△ADM,△AEF,△ABN.
(2)∵△AMN∽△BME,
∴$\frac{AM}{BM}$=$\frac{MN}{ME}$,
∴$\frac{AM}{MN}$=$\frac{BM}{ME}$,∵∠AMB=∠EMN,
∴△AMB∽△NME,
∴∠AEN=∠ABD=45°,∵∠EAN=45°,
∴∠NAE=∠NEA=45°,
∴△AEN是等腰直角三角形,
∴AE=$\sqrt{2}$AN,
∵△AMN∽△BME,△AFE∽△BME,
∴△AMN∽△AFE,
∴$\frac{MN}{EF}$=$\frac{AN}{AE}$=$\frac{1}{\sqrt{2}}$,
∴EF=$\sqrt{2}$MN.
(3))∵△AMN∽△BME,
∴$\frac{AM}{BM}$=$\frac{MN}{ME}$,
∴$\frac{AM}{MN}$=$\frac{BM}{ME}$,∵∠AMB=∠EMN,
∴△AMB∽△NME,
∴∠AEN=∠ABD=45°,∵∠EAN=45°,
∴∠NAE=∠NEA=45°,
∴△AEN是等腰直角三角形.
点评 本题考查相似三角形的判定和性质、全等三角形的判定和性质,等腰直角三角形的判定和性质等知识,解题的关键是灵活应用所学知识解决问题,学会添加常用辅助线构造全等三角形,学会利用相似三角形的性质解决线段之间的关系问题,属于中考压轴题.

 状元坊全程突破导练测系列答案
状元坊全程突破导练测系列答案 直通贵州名校周测月考直通名校系列答案
直通贵州名校周测月考直通名校系列答案| A. | -2 | B. | 2 | C. | 28 | D. | -28 |
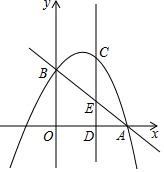 如图,直线y=-x+2与x轴、y轴分别相交于A、B两点,抛物线y=-x2+bx+c经过点A和点B,C是第一象限内抛物线上的一动点,过点C作CD⊥x轴于点D,交直线AB于点E.
如图,直线y=-x+2与x轴、y轴分别相交于A、B两点,抛物线y=-x2+bx+c经过点A和点B,C是第一象限内抛物线上的一动点,过点C作CD⊥x轴于点D,交直线AB于点E. 由一些大小相同的小正方形搭成的几何体的俯视图,如图所示,其中正方形中的数字表示该位置上的小正方形的个数,请画出该几何体的主视图和左视图.
由一些大小相同的小正方形搭成的几何体的俯视图,如图所示,其中正方形中的数字表示该位置上的小正方形的个数,请画出该几何体的主视图和左视图.