题目内容
10.一次函数y=kx+b,当1≤x≤4时,3≤y≤6,求$\frac{b}{k}$的值.分析 分k>0、k<0两种情况考虑,根据一次函数的性质找出点的坐标,利用待定系数法求出k、b值,再将其代入$\frac{b}{k}$中即可得出结论.
解答 解:当k>0时,y值随x值的增大而增大,
∴$\left\{\begin{array}{l}{3=k+b}\\{6=4k+b}\end{array}\right.$,解得:$\left\{\begin{array}{l}{k=1}\\{b=2}\end{array}\right.$,
此时$\frac{b}{k}$=2;
当k<0时,y值随x值的增大减小,
∴$\left\{\begin{array}{l}{6=k+b}\\{3=4k+b}\end{array}\right.$,解得:$\left\{\begin{array}{l}{k=-1}\\{b=7}\end{array}\right.$,
此时$\frac{b}{k}$=-7.
综上所述:$\frac{b}{k}$的值为2或-7.
点评 本题考查了一次函数的性质以及待定系数法求一次函数解析式,分k>0、k<0两种情况考虑是解题的关键.

练习册系列答案
相关题目
6.已知-1<x<0,那么在x、2x、$\sqrt{(-x)}$、-x2中最小的数是( )
| A. | -x2 | B. | 2x | C. | $\sqrt{(-x)}$ | D. | x |
4.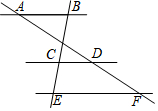 如图,已知AB∥CD∥EF,AD:AF=3:5,BE=15,那么CE的长等于( )
如图,已知AB∥CD∥EF,AD:AF=3:5,BE=15,那么CE的长等于( )
 如图,已知AB∥CD∥EF,AD:AF=3:5,BE=15,那么CE的长等于( )
如图,已知AB∥CD∥EF,AD:AF=3:5,BE=15,那么CE的长等于( )| A. | 9 | B. | 6 | C. | $\frac{15}{2}$ | D. | $\frac{9}{2}$ |
 如图,在矩形OABC中,OA=8,OC=4,OA、OC分别在x轴与y轴上,D为OA上一点,且CD=AD.
如图,在矩形OABC中,OA=8,OC=4,OA、OC分别在x轴与y轴上,D为OA上一点,且CD=AD.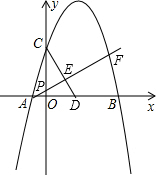 如图,已知抛物线y=ax2+bx+3与x轴交于A,B两点(点A在原点左侧,点B在原点右侧),与y轴交于点C,且OB=OC=3OA,点P为线段OC上一动点,射线AP与抛物线交于点F,CD⊥AF于点E,交x轴于点D.
如图,已知抛物线y=ax2+bx+3与x轴交于A,B两点(点A在原点左侧,点B在原点右侧),与y轴交于点C,且OB=OC=3OA,点P为线段OC上一动点,射线AP与抛物线交于点F,CD⊥AF于点E,交x轴于点D.