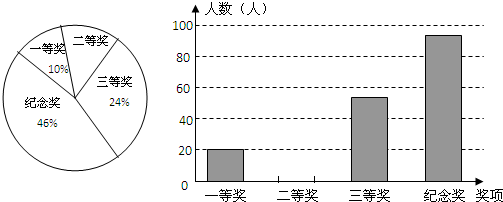
题目内容
20.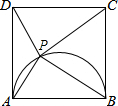 如图,已知四边形ABCD是边长为4的正方形,以AB为直径向正方形内作半圆,P为半圆上一动点(不与A、B重合),当PA=2$\sqrt{2}$或$\frac{8\sqrt{5}}{5}$时,△PAD为等腰三角形.
如图,已知四边形ABCD是边长为4的正方形,以AB为直径向正方形内作半圆,P为半圆上一动点(不与A、B重合),当PA=2$\sqrt{2}$或$\frac{8\sqrt{5}}{5}$时,△PAD为等腰三角形.
分析 分别从当PA=PD,PA=AD,AD=PD时,△PAD是等腰三角形讨论,然后由等腰三角形的性质与射影定理即可求得答案.
解答 解:①当PA=PD时,
此时P位于四边形ABCD的中心,
过点P作PE⊥AD于E,作PM⊥AB于M,
则四边形EAMP是正方形,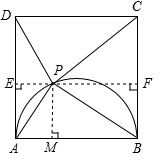
∴PM=PE=$\frac{1}{2}$AB=2,
∵PM2=AM•BM=4,
∵AM+BM=4,
∴AM=2,
∴PA=2$\sqrt{2}$,
②当PA=AD时,PA=4(舍);
③当PD=DA时,以点D为圆心,DA为半径作圆与弧AB的交点为点P.
连PD,令AB中点为O,再连DO,PO,DO交AP于点G,
则△ADO≌△PDO,
∴DO⊥AP,AG=PG,
∴AP=2AG,
又∵DA=2AO,
∴AG=2OG,
设AG为2x,OG为x,
∴(2x)2+x2=4,
∴x=$\frac{2\sqrt{5}}{5}$,
∴AG=2x=$\frac{4\sqrt{5}}{5}$,
∴PA=2AG=$\frac{8\sqrt{5}}{5}$;
∴PA=2$\sqrt{2}$或4或$\frac{8\sqrt{5}}{5}$,
故答案为:2$\sqrt{2}$或$\frac{8\sqrt{5}}{5}$.
点评 此题考查了正方形的性质,圆周角的性质以及勾股定理等知识.此题综合性很强,解题时要注意数形结合与方程思想的应用.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
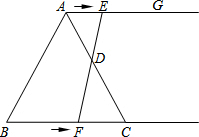 如图,在等边三角形ABC中,BC=6cm,射线AG∥BC,点E从点A出发沿射线AG以1cm/s的速度运动,同时点F从点B出发沿射线BC以2cm/s的速度运动,设运动时间为ts.
如图,在等边三角形ABC中,BC=6cm,射线AG∥BC,点E从点A出发沿射线AG以1cm/s的速度运动,同时点F从点B出发沿射线BC以2cm/s的速度运动,设运动时间为ts.
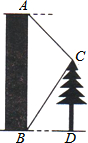 如图,某建筑物AB的高为6米,在建筑物顶端A测得一棵树CD的点C的俯角为45°,在地面点B测得点C的仰角为60°,求树高CD(结果精确到0.1米).(参考数据:$\sqrt{3}$≈1.7,$\sqrt{2}$≈1.4)
如图,某建筑物AB的高为6米,在建筑物顶端A测得一棵树CD的点C的俯角为45°,在地面点B测得点C的仰角为60°,求树高CD(结果精确到0.1米).(参考数据:$\sqrt{3}$≈1.7,$\sqrt{2}$≈1.4)