题目内容
5. 如图,CD是Rt△ABC斜边上的高,∠ACB=90°,BC=2,AB=3.
如图,CD是Rt△ABC斜边上的高,∠ACB=90°,BC=2,AB=3.(1)求证:CD2=AD•BD;
(2)请直接写出△ACD与△CBD的周长比=$\frac{\sqrt{5}}{2}$.
△ACD与△CBD的面积比=$\frac{5}{4}$.
分析 (1)证明△ACD∽△CBD,然后根据相似三角形的对应边的比相等即可证得;
(2)根据相似三角形的性质即可得到结论.
解答 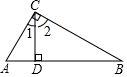 证明:∵Rt△ABC中,∠ACB=90°,
证明:∵Rt△ABC中,∠ACB=90°,
∴∠1+∠2=90°,
又∵CD是斜边AB上的高
∴∠ADC=∠CDB=90°,
∴∠1+∠A=90°,
∴∠A=∠2,
∴△ACD∽△CBD,
∴$\frac{AD}{CD}=\frac{CD}{BD}$,
∴CD2=AD•BD;
(2)∵∠ACB=90°,BC=2,AB=3,
∴AC=$\sqrt{5}$,
∴△ACD与△CBD的周长比=$\frac{AC}{BC}$=$\frac{\sqrt{5}}{2}$,△ACD与△CBD的面积比=($\frac{AC}{BC}$)2=$\frac{5}{4}$.
故答案为:$\frac{\sqrt{5}}{2}$,$\frac{5}{4}$.
点评 本题考查了相似三角形的判定与性质,证明等积式成立,常用的思路就是转化为证明比例式,从而转化为证明三角形相似.

练习册系列答案
相关题目
18.对于二次函数y=2x2-4x-6,下列说法正确的是( )
| A. | 图象的开口向下 | B. | 当x>1时,y随x的增大而减小 | ||
| C. | 当x<1时,y随x的增大而减小 | D. | 图象的对称轴是直线x=-1 |
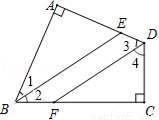
17.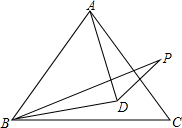 如图所示,在等边△ABC中,BD平分∠PBC,且DB=DA,则∠BPD的度数是( )
如图所示,在等边△ABC中,BD平分∠PBC,且DB=DA,则∠BPD的度数是( )
 如图所示,在等边△ABC中,BD平分∠PBC,且DB=DA,则∠BPD的度数是( )
如图所示,在等边△ABC中,BD平分∠PBC,且DB=DA,则∠BPD的度数是( )| A. | 20° | B. | 30° | C. | 40° | D. | 无法计算 |
13.小强以5km/h的速度出发,16min后小明从同一地点出发,以13km/h的速度追赶小强,则小明从出发到追上小强所用的时间为( )
| A. | $\frac{1}{6}$h | B. | 10h | C. | $\frac{80}{13}$ | D. | 以上答案都不对 |
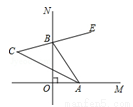
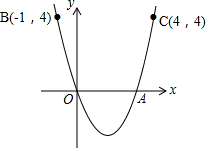 如图,抛物线y=ax2+bx经过原点O,与x轴的另一个交点是A点,点B(-1,4)和点C(4,4)是抛物线上的两个点,则点A的坐标为(3,0).
如图,抛物线y=ax2+bx经过原点O,与x轴的另一个交点是A点,点B(-1,4)和点C(4,4)是抛物线上的两个点,则点A的坐标为(3,0). 的图象,当
的图象,当 时,
时, 随
随 的增大而减小,则
的增大而减小,则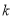 的取值范围是( )
的取值范围是( ) B.
B.  C.
C. 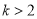 D.
D. 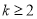
 (2)
(2) 