题目内容
20．
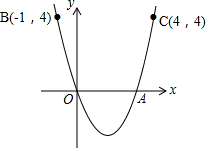如图，抛物线y=ax2+bx经过原点O，与x轴的另一个交点是A点，点B（-1，4）和点C（4，4）是抛物线上的两个点，则点A的坐标为（3，0）．
分析 根据条件可得对称性x=$\frac{3}{2}$，再根据对称性可以求出点A坐标．
解答 解：∵点B（-1，4）和点C（4，4）是抛物线上的两个点，
∴抛物线的对称轴是x=$\frac{3}{2}$，
∵A、O关于对称轴对称，
∴A（3，0）．
故答案为（3，0）．
点评 本题考查抛物线与x轴的交点，解题的关键是灵活运用所学知识解决问题，确定对称性的位置是本题的突破点，属于中考常考题型．
练习册系列答案
口算题卡河北少年儿童出版社系列答案
A加金题 系列答案
全优测试卷系列答案
相关题目
12．下列方程是关于x的一元二次方程的是（ ）
| A． | ax2+bx+c=0 | B． | $\frac{1}{{x}^{2}}$+$\frac{1}{x}$=2 | C． | x2+2x=x2-1 | D． | 3（x+1）2=2（x+1） |
8．
如图，△ABC内接于⊙O，AB是⊙O的直径，∠B=30°，CE平分∠ACB交⊙O于E，交AB于点D，连接AE，则AE：BC的值等于（ ）
如图，△ABC内接于⊙O，AB是⊙O的直径，∠B=30°，CE平分∠ACB交⊙O于E，交AB于点D，连接AE，则AE：BC的值等于（ ）| A． | 1：$\sqrt{2}$ | B． | $\sqrt{2}$：$\sqrt{3}$ | C． | $\sqrt{2}$：2 | D． | 2：3 |
15．已知点A在半径为3的圆上，则点A与圆心O的距离d=（ ）
| A． | 2 | B． | 3 | C． | 4 | D． | 5 |
如图，CD是Rt△ABC斜边上的高，∠ACB=90°，BC=2，AB=3．
元，选择乙商场时，所需费用为
元，请分别写出
， 
与x之间的关系式；