题目内容
3个边长2厘米的正方形如图，甲的中心在乙的一个顶点上，乙的中心在丙的一个顶点上，甲与丙不重叠．则甲乙丙总共覆盖的面积是________平方厘米．
10
分析：首先确定甲乙与乙丙重合部分相等，且为四分之一个正方形面积，则可求得甲乙丙总共覆盖的面积．
解答：
解：∵图中两个涂色的三角形面积相同，
∴甲、乙重合部分面积=四分之一个正方形面积=22÷4=1．
同理乙，丙重合部分面积=1，
∴甲乙丙总共覆盖面积=3×22-2×1=10平方厘米．
故答案为：10．
点评：此题考查了正方形的性质．解此题的关键是找到甲乙与乙丙重合部分相等，且为四分之一个正方形面积．
分析：首先确定甲乙与乙丙重合部分相等，且为四分之一个正方形面积，则可求得甲乙丙总共覆盖的面积．
解答：
解：∵图中两个涂色的三角形面积相同，∴甲、乙重合部分面积=四分之一个正方形面积=22÷4=1．
同理乙，丙重合部分面积=1，
∴甲乙丙总共覆盖面积=3×22-2×1=10平方厘米．
故答案为：10．
点评：此题考查了正方形的性质．解此题的关键是找到甲乙与乙丙重合部分相等，且为四分之一个正方形面积．
练习册系列答案
名题金卷系列答案
相关题目
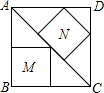把边长为40厘米的正方形ABCD沿对角线AC截成两个三角形，在两个三角形内如图所示剪下两个内接正方形M、N，则M、N的面积的差是
分的面积（用a，b表示），并求当a=14.6，b=2.7时，剩余部分的面积为多少平方厘米？
3个边长2厘米的正方形如图，甲的中心在乙的一个顶点上，乙的中心在丙的一个顶点上，甲与丙不重叠．则甲乙丙总共覆盖的面积是