题目内容
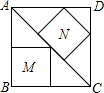 把边长为40厘米的正方形ABCD沿对角线AC截成两个三角形,在两个三角形内如图所示剪下两个内接正方形M、N,则M、N的面积的差是
把边长为40厘米的正方形ABCD沿对角线AC截成两个三角形,在两个三角形内如图所示剪下两个内接正方形M、N,则M、N的面积的差是分析:分别求出正方形M和正方形N的面积,用大正方形的面积减去小正方形的面积即可求解.
解答:解:正方形M的面积=20cm×20cm=400cm2,
设:正方形N的边长为x,则存在:
x2+
×x2+
×x2+
×
×x2=
,
解得:x2=
cm2,
故M、N的面积的差为(400-
)cm2=
cm2.
故答案为:
cm2.
设:正方形N的边长为x,则存在:
x2+
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 40×40 |
| 2 |
解得:x2=
| 3200 |
| 9 |
故M、N的面积的差为(400-
| 3200 |
| 9 |
| 400 |
| 9 |
故答案为:
| 400 |
| 9 |
点评:本题考查了正方形,等腰三角形面积的计算方法,考查了正方形四边相等,各内角均为直角的性质,解本题的关键是正方形N的面积的计算.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 如图,小明把一张边长为10厘米的正方形硬纸板的四周各剪去一个同样大小的正方形,再折合成一个无盖的长方体盒子,
如图,小明把一张边长为10厘米的正方形硬纸板的四周各剪去一个同样大小的正方形,再折合成一个无盖的长方体盒子, (2013•香坊区一模)如图,在一个边长为40厘米的正方形硬纸板的四角各剪一个边长为xcm的小正方形,将剩余部分折成一个无盖的长方体盒子(纸板的厚度忽略不计),设折成的长方体盒子的侧面积为Scm2.
(2013•香坊区一模)如图,在一个边长为40厘米的正方形硬纸板的四角各剪一个边长为xcm的小正方形,将剩余部分折成一个无盖的长方体盒子(纸板的厚度忽略不计),设折成的长方体盒子的侧面积为Scm2.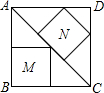 把边长为40厘米的正方形ABCD沿对角线AC截成两个三角形,在两个三角形内如图所示剪下两个内接正方形M、N,则M、N的面积的差是________平方厘米.
把边长为40厘米的正方形ABCD沿对角线AC截成两个三角形,在两个三角形内如图所示剪下两个内接正方形M、N,则M、N的面积的差是________平方厘米.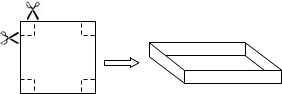 如图,在一个边长为40厘米的正方形硬纸板的四角各剪一个边长为xcm的小正方形,将剩余部分折成一个无盖的长方体盒子(纸板的厚度忽略不计),设折成的长方体盒子的侧面积为Scm2.
如图,在一个边长为40厘米的正方形硬纸板的四角各剪一个边长为xcm的小正方形,将剩余部分折成一个无盖的长方体盒子(纸板的厚度忽略不计),设折成的长方体盒子的侧面积为Scm2. 时,二次函数y=ax2+bx+c(a≠0)有最小(大)值
时,二次函数y=ax2+bx+c(a≠0)有最小(大)值 】
】