题目内容

13．若a、b、c为三角形的三边长，且a、b满足|a-3|+（b-2）2=0，则第三边长c的取值范围是1＜c＜5．

分析 先根据非负数的性质求出a、b的值，再由三角形的三边关系即可得出结论．

解答 解：∵a、b满足|a-3|+（b-2）2=0，
∴a-3=0，b-2=0，
∴a=3，b=2．
∵a、b、c为三角形的三边长，
∴3-2＜c＜3+2，即1＜c＜5．
故答案为：1＜c＜5．

点评 本题考查的是三角形的三边关系，熟知三角形任意两边之和大于第三边，任意两边之差小于第三边是解答此题的关键．

练习册系列答案
相关题目
3．连续抛掷一枚质地均匀的一元硬币100次出现了100次正面朝上，则第101次抛掷该硬币出现正面朝上的概率是$\frac{1}{2}$．
4．计算（-1）2017+$（\frac{1}{3}）^{-2}$-3÷（2017-π）0的结果是5．
1．已知方程组$\left\{\begin{array}{l}{2x+y=-2}\\{ax-by=-4}\end{array}\right.$和方程组$\left\{\begin{array}{l}{3x-y=12}\\{bx+ay=-8}\end{array}\right.$的解相同，求a、b的值．
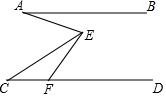8．如图，已知AB∥CD，F为CD上一点，∠EFD=60°，∠AEC=2∠CEF，若6°＜∠BAE＜15°，∠C的度数为整数，则∠C的度数为36°或37°．
18．某商家预测一种应季衬衫能畅销市场，就先用10000元购进了一批这种衬衫，面市后的确供不应求，于是商家又用21600元购进了第二批这种衬衫，所购数量是第一批购进量的2倍，但单价贵了10元．
（1）该商家购进的第一批衬衫是多少件？
（2）若两批衬衫按相同的标价销售，最后剩下30件按八折优惠卖出，全部售完后纯利润为10520元（不考虑其他因素），求每件衬衫的标价是多少元？
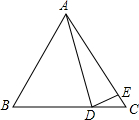5．如图，△ABC中，∠B=65°，∠BAD=40°，∠AED=100°，∠CDE=45°，求∠CAD的度数．
2．某校八年级全体同学参加了某项捐款活动，随机抽查了部分同学捐款的情况，并统计绘制成了如图两幅不完整的条形统计图和扇形统计图，请根据所提供的信息，解答下列问题：
（1）本次共抽查学生50人，并将条形图补充完整；
（2）捐款金额的众数是10，中位数是12.5；
（3）在八年级850名学生中，捐款20元及以上（含20元）的学生估计有多少人？
1．已知x＜y，则下列式子不正确的是（　　）
A．4x＜4yB．-4x＜-4yC．x+4＜y+4D．x-4＜y-4

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网