题目内容
6.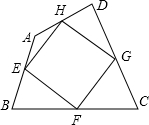 已知四边形ABCD中,E、F、G、H分别为AB、BC、CD、DA的中点,当四边形ABCD的对角线AC、BD满足AC=BD时,四边形EFGH是菱形.
已知四边形ABCD中,E、F、G、H分别为AB、BC、CD、DA的中点,当四边形ABCD的对角线AC、BD满足AC=BD时,四边形EFGH是菱形.
分析 根据三角形中位线定理得到EH=$\frac{1}{2}$BD,FG=$\frac{1}{2}$BD,EH∥BD,FG∥BD,HG=$\frac{1}{2}$AC,证明四边形EFGH是平行四边形,根据菱形的判定定理解答即可.
解答 解: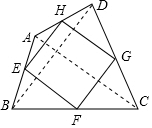 连接AC、BD,
连接AC、BD,
∵E、F、G、H分别为AB、BC、CD、DA的中点,
∴EH=$\frac{1}{2}$BD,FG=$\frac{1}{2}$BD,EH∥BD,FG∥BD,HG=$\frac{1}{2}$AC,
∴EH=FG,EH∥FG,
∴四边形EFGH是平行四边形,
当AC=BD时,HE=HG,
∴四边形EFGH是菱形,
故答案为:AC=BD.
点评 本题考查的是中点四边形,掌握三角形中位线定理、菱形的判定定理是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
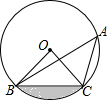 如图,点A、B、C在⊙O上,若∠BAC=45°,OB=2,则图中阴影部分的面积为π-2(结果保留π)
如图,点A、B、C在⊙O上,若∠BAC=45°,OB=2,则图中阴影部分的面积为π-2(结果保留π) 如图,一张三角形纸片ABC,∠B=45°,现将纸片的一角向内折叠,折痕ED∥BC,则∠AEB的度数为90°.
如图,一张三角形纸片ABC,∠B=45°,现将纸片的一角向内折叠,折痕ED∥BC,则∠AEB的度数为90°.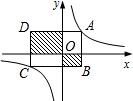 如图,在平面直角坐标系中,面积为a的矩形ABCD的边与坐标轴平行或垂直,顶点A、C分别在函数y=$\frac{1}{x}$的图象的两个分支上,则图中两块阴影部分面积的和等于a-2.(用含a的式子表示)
如图,在平面直角坐标系中,面积为a的矩形ABCD的边与坐标轴平行或垂直,顶点A、C分别在函数y=$\frac{1}{x}$的图象的两个分支上,则图中两块阴影部分面积的和等于a-2.(用含a的式子表示)