��Ŀ����
��֪����y=��x+4��ͼ���뺯��
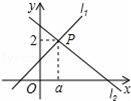
 ��ͼ����ͬһ����ϵ�ڣ�����y=��x+4��ͼ����ͼ1�������ύ��A��B���㣬��M��2��m����ֱ��AB��һ�㣬��N���M����y��Գƣ��߶�MN��y���ڵ�C��
��ͼ����ͬһ����ϵ�ڣ�����y=��x+4��ͼ����ͼ1�������ύ��A��B���㣬��M��2��m����ֱ��AB��һ�㣬��N���M����y��Գƣ��߶�MN��y���ڵ�C��
��1��m=��������������S��AOB=��������������
��2������߶�MN������������
 ��ͼ��ֳ������֣������������ֳ��ȵı�Ϊ1��3����k��ֵ��
��ͼ��ֳ������֣������������ֳ��ȵı�Ϊ1��3����k��ֵ��
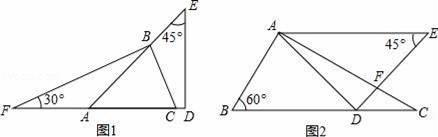
��3����ͼ2��������������
 ͼ����N����ʱ�����������ϴ���������E��x1��y1����F��x2��y2������ԭ��Գ��ҵ�ֱ��MN�ľ���֮��Ϊ1��3����x1��x2��ֱ��д������������꣮
ͼ����N����ʱ�����������ϴ���������E��x1��y1����F��x2��y2������ԭ��Գ��ҵ�ֱ��MN�ľ���֮��Ϊ1��3����x1��x2��ֱ��д������������꣮


�����㡿�����������ۺ��⣮
����������1�����õ��ں���ͼ���ϵ��ص����m���Լ�ƽ��ֱ������ϵ�������ε�����ļ��㷽���������������ƽ�����������ֱ���ϵı���Ϊ�ף���
��2�����õ�ĶԳƵ�������ص����N������꣬�߶�MN������������
 ��ͼ��ֳ������֣������������ֳ��ȵı�Ϊ1��3���ҽ���ΪD�����������
��ͼ��ֳ������֣������������ֳ��ȵı�Ϊ1��3���ҽ���ΪD�����������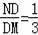
 ��
��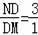
 ���㼴�ɣ�
���㼴�ɣ�
��3�����õ㵽ƽ�����������ֱ�ߵľ���ļ��㷽���Լ��ͣ�2�����Ƶķ������������������ȡ����ֵʱ��ҲҪ��������㣮
����𡿽⣺��1����M��2��m����ֱ��y=��x+4��ͼ���ϣ�
��m=��2+4=2��
����y=��x+4��ͼ���������ύ��A��B���㣬
��A��4��0����B��0��4����
��OA=4��OB=4��
��S��AOB=
 OA��OB=
OA��OB=
 ��4��4=8��
��4��4=8��
�ʴ�Ϊm=2��S��AOB=8��
��2����m=2��
��M��2��2����
�ߵ�N���M����y��Գƣ�
��N����2��2����
��MN=4��
���߶�MN������������
 ��ͼ��ֳ������֣������������ֳ��ȵı�Ϊ1��3���ҽ���ΪD��
��ͼ��ֳ������֣������������ֳ��ȵı�Ϊ1��3���ҽ���ΪD��
�ٵ�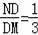
 ʱ������
ʱ������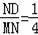
 ��
��
��ND=1��
��D����1��2����
��k=��1��2=��2��
�ڵ�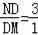
 ʱ������
ʱ������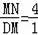
 ��
��
��DM=
 MN=
MN=
 ��4=1��
��4=1��
��D��1��2����
��k=1��2=2��
��k��ֵΪ��2��2��
��3������������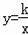
 ͼ����N����N����2��2����
ͼ����N����N����2��2����
��k=��2��2=��4��
�߷����������ϴ���������E��x1��y1����F��x2��y2����
��x1y1=��4x2��y2=��4��
�ߵ�E��x1��y1����F��x2��y2������ԭ��Գƣ�
��x2=��x1��y2=��y1��
��M��2��2����N����2��2����
���E��ֱ��MN�ľ���Ϊ|y1��2|����F��ֱ��MN�ľ���Ϊ|y1+2|��
�ߵ�E��x1��y1����F��x2��y2����ֱ��MN�ľ���֮��Ϊ1��3��
���E��x1��y1����F����x1����y1����ֱ��MN�ľ���֮��Ϊ1��3��
�ٵ�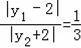
 ʱ������3|y1��2|=|y1+2|
ʱ������3|y1��2|=|y1+2|
��y1��2ʱ��3y1��6=y1+2��
��y1=4��
��y2=��4��x1=��1��x2=1
����2��y1��2ʱ����3y1+6=y1+2��
��y1=1��
��y2=��1��x1=��4��x2=4
��y1�ܩ�2ʱ����3y1+6=��y1+2��
��y1=2���ᣩ��
�ڵ�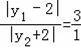
 ʱ������3|y1+2|=|y1��2|��
ʱ������3|y1+2|=|y1��2|��
��y1��2ʱ��3y1+6=y1��2��
��y1=��4���ᣩ��
����2��y1��2ʱ��3y1+6=��y1+2��
��y1=��1��
��y2=1��x1=4��x2=��4����x1��x2���ᣩ��
��y1�ܩ�2ʱ����3y1��6=��y1+2��
��y1=��4��
��y2=4��x1=1��x2=��1����x1��x2���ᣩ��
��E����4��1����F��1����4��
E����4��1����F��4����1��
�������������Ƿ�����������һ���ۺ��⣬��Ҫ�����˵��ں���ͼ���ϵ��ص㣬�����m������ϵ�м�������������ķ�������������������֮��ľ���͵㵽ֱ�ߵľ��룬�����ND��MD����E��F��ֱ��MN�ľ��룬����Ĺؼ���ȷ��ȷ������ľ���͵㵽ֱ�ߵľ����ȷ�������õ��˷ּ���������㣬��������һ�������

 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
 |+2��
|+2��
 ��3
��3