题目内容
计算:(
)n×5n+2= ,(x2y)2n•(xy)n-1= .
| 1 |
| 5 |
考点:幂的乘方与积的乘方,单项式乘单项式
专题:
分析:根据同底数幂的乘法,可得指数相同的幂的乘法,根据积的乘方,可得答案;
根据幂的乘方,可得同底数幂的乘法,根据同底数幂的乘法,可得答案.
根据幂的乘方,可得同底数幂的乘法,根据同底数幂的乘法,可得答案.
解答:解:原式=(
)n×5n×52=(
×5)n×52=25,
原式=x4ny2n•xn-1yn-1=x4n+n-1y2n+n-1=x5n-1y3n-1,
故答案为:25,x5n-1y3n-1.
| 1 |
| 5 |
| 1 |
| 5 |
原式=x4ny2n•xn-1yn-1=x4n+n-1y2n+n-1=x5n-1y3n-1,
故答案为:25,x5n-1y3n-1.
点评:本题考查了幂的乘方与积的乘方,第一个先化成积的乘方是解题关键,第二个先求积的乘方再求同底数幂的乘法.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
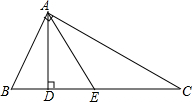 如图所示,已知AD,AE分别是△ABC和△ADC的高和中线,AB=6cm,AC=8cm,BC=10cm,∠CAB=90°.试求:
如图所示,已知AD,AE分别是△ABC和△ADC的高和中线,AB=6cm,AC=8cm,BC=10cm,∠CAB=90°.试求: 有一块长100米,宽50米的矩形花园,要在其中修两条如图所示的宽度相同的道路,剩下的部分种植花草,已知种植花草的面积为4704米2,求道路的宽.
有一块长100米,宽50米的矩形花园,要在其中修两条如图所示的宽度相同的道路,剩下的部分种植花草,已知种植花草的面积为4704米2,求道路的宽.