题目内容
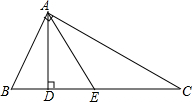 如图所示,已知AD,AE分别是△ABC和△ADC的高和中线,AB=6cm,AC=8cm,BC=10cm,∠CAB=90°.试求:
如图所示,已知AD,AE分别是△ABC和△ADC的高和中线,AB=6cm,AC=8cm,BC=10cm,∠CAB=90°.试求:(1)AD的长;
(2)△ABE的面积;
(3)△ACE和△ABE的周长的差.
考点:三角形的角平分线、中线和高,三角形的面积
专题:
分析:(1)利用“面积法”来求线段AD的长度;
(2)△AEC与△ABE是等底同高的两个三角形,它们的面积相等;
(3)由于AE是中线,那么BE=CE,于是△ACE的周长-△ABE的周长=AC+AE+CE-(AB+BE+AE),化简可得△ACE的周长-△ABE的周长=AC-AB,易求其值.
(2)△AEC与△ABE是等底同高的两个三角形,它们的面积相等;
(3)由于AE是中线,那么BE=CE,于是△ACE的周长-△ABE的周长=AC+AE+CE-(AB+BE+AE),化简可得△ACE的周长-△ABE的周长=AC-AB,易求其值.
解答:解:∵∠BAC=90°,AD是边BC上的高,
∴
AB•AC=
BC•AD,
∴AD=
=
=4.8(cm),即AD的长度为4.8cm;
(2)如图,∵△ABC是直角三角形,∠BAC=90°,AB=6cm,AC=8cm,
∴S△ABC=
AB•AC=
×6×8=24(cm2).
又∵AE是边BC的中线,
∴BE=EC,
∴
BE•AD=
EC•AD,即S△ABE=S△AEC,
∴S△ABE=
S△ABC=12(cm2).
∴△ABE的面积是12cm2.
(3)∵AE为BC边上的中线,
∴BE=CE,
∴△ACE的周长-△ABE的周长=AC+AE+CE-(AB+BE+AE)=AC-AB=8-6=2(cm),即△ACE和△ABE的周长的差是2cm.
∴
| 1 |
| 2 |
| 1 |
| 2 |
∴AD=
| AB•AC |
| BC |
| 6×8 |
| 10 |
(2)如图,∵△ABC是直角三角形,∠BAC=90°,AB=6cm,AC=8cm,
∴S△ABC=
| 1 |
| 2 |
| 1 |
| 2 |
又∵AE是边BC的中线,
∴BE=EC,
∴
| 1 |
| 2 |
| 1 |
| 2 |
∴S△ABE=
| 1 |
| 2 |
∴△ABE的面积是12cm2.
(3)∵AE为BC边上的中线,
∴BE=CE,
∴△ACE的周长-△ABE的周长=AC+AE+CE-(AB+BE+AE)=AC-AB=8-6=2(cm),即△ACE和△ABE的周长的差是2cm.
点评:本题考查了中线的定义、三角形周长的计算.解题的关键是利用三角形面积的两个表达式相等,求出AD.

练习册系列答案
 期末集结号系列答案
期末集结号系列答案
相关题目
 如图,⊙O的两弦AB,CD垂直相交于点E,试判断∠AOC与∠?BOD的关系并给出证明.
如图,⊙O的两弦AB,CD垂直相交于点E,试判断∠AOC与∠?BOD的关系并给出证明. 如图,在扇形OAB中,∠AOB=105°,半径OA=10,将扇形OAB沿过点B的直线折叠,点O恰好落在弧AB上的点D处,折痕BC交OA于点C,则图中阴影部分面积是多少?
如图,在扇形OAB中,∠AOB=105°,半径OA=10,将扇形OAB沿过点B的直线折叠,点O恰好落在弧AB上的点D处,折痕BC交OA于点C,则图中阴影部分面积是多少? 如图所示,∠3+∠4=180°,则∠1
如图所示,∠3+∠4=180°,则∠1 已知,如图,AD∥BC,∠1=∠2,∠3=∠E.试说明:AE∥CD.
已知,如图,AD∥BC,∠1=∠2,∠3=∠E.试说明:AE∥CD.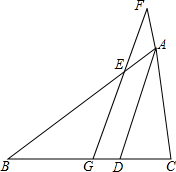 △ABC中,AD是∠BAC的平分线,G是BC的中点,过G作直线FG平行于AD,分别交AB和CA的延长线于点E和点F,求证:BE=CF=
△ABC中,AD是∠BAC的平分线,G是BC的中点,过G作直线FG平行于AD,分别交AB和CA的延长线于点E和点F,求证:BE=CF=