题目内容
 如图,在△ABC中,AB=AC=13,BC=10,点D为BC的中点,DE⊥AB,垂足为点E,求DE的长.
如图,在△ABC中,AB=AC=13,BC=10,点D为BC的中点,DE⊥AB,垂足为点E,求DE的长.考点:勾股定理,等腰三角形的性质
专题:
分析:首先连接AD,由△ABC中,AB=AC=13,BC=10,D为BC中点,利用等腰三角形的三线合一的性质,即可证得:AD⊥BC,然后利用勾股定理,即可求得AD的长,然后利用面积法来求DE的长.
解答: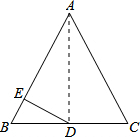 解:连接AD,
解:连接AD,
∵△ABC中,AB=AC=13,BC=10,D为BC中点,
∴AD⊥BC,BD=
BC=5,
∴AD=
=12,
又∵DE⊥AB,
∴
BD•AD=
AB•ED,
∴ED=
=
=,
解得:DE=
.
 解:连接AD,
解:连接AD,∵△ABC中,AB=AC=13,BC=10,D为BC中点,
∴AD⊥BC,BD=
| 1 |
| 2 |
∴AD=
| AB2-BD2 |
又∵DE⊥AB,
∴
| 1 |
| 2 |
| 1 |
| 2 |
∴ED=
| BD•AD |
| AB |
| 5×12 |
| 13 |
解得:DE=
| 60 |
| 13 |
点评:此题考查了等腰三角形的性质以及勾股定理.此题难度适中,解题的关键是准确作出辅助线,注意数形结合思想的应用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
若抛物线y=ax2+b不经过第三、四象限,则抛物线y=ax2+bx+c( )
| A、开口向上,对称轴是y轴 |
| B、开口向下,对称轴是y轴 |
| C、开口向上,对称轴平行于y轴 |
| D、开口向下,对称轴平行于y轴 |
下列说法正确的是( )
| A、1的平方根是1 | |||
| B、-1的立方根是-1 | |||
C、
| |||
D、-2是
|
点P1(x1,y1),点P2(x2,y2)是一次函数y=-2x-3图象上的两个点,且x1<x2,则y1与y2的大小关系是( )
| A、y1>y2 |
| B、y1>y2>0 |
| C、y1<y2 |
| D、y1=y2 |
 如图,反比例函数
如图,反比例函数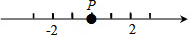 某校为培育青少年科技创新能力,举办了动漫制作活动,小明设计了点P在数轴上做直线运动的一个雏形,如图所示.点P从原点开始运动至停止的记录为:+12,-8,-2,-7,+3.问:当运动停止时,点P位置上的数是多少?
某校为培育青少年科技创新能力,举办了动漫制作活动,小明设计了点P在数轴上做直线运动的一个雏形,如图所示.点P从原点开始运动至停止的记录为:+12,-8,-2,-7,+3.问:当运动停止时,点P位置上的数是多少? 如图,点A、B分别在二次函数y=x2的图象上,且线段AB⊥y轴,若AB=6,试求点A、B的坐标.
如图,点A、B分别在二次函数y=x2的图象上,且线段AB⊥y轴,若AB=6,试求点A、B的坐标.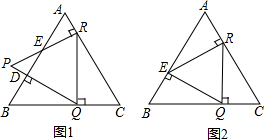 如图1,D是边长为8cm的等边△ABC的边AB上的一点,DQ⊥AB交边BC于点Q,RQ⊥BC交边AC于点R,RP⊥AC交边AB于点E,交QD的延长线于点P.
如图1,D是边长为8cm的等边△ABC的边AB上的一点,DQ⊥AB交边BC于点Q,RQ⊥BC交边AC于点R,RP⊥AC交边AB于点E,交QD的延长线于点P.