题目内容
8. 如图,∠BOC=60°,点A是BO延长线上的一点,OA=10cm,动点P从点A出发沿AB以2cm/s的速度移动,动点Q从点O出发沿OC以1cm/s的速度移动,如果点P,Q同时出发,用t(s)表示移动的时间,当t=$\frac{10}{3}$或10s时,△POQ是等腰三角形;当t=$\frac{20}{3}$s时,△POQ是直角三角形.
如图,∠BOC=60°,点A是BO延长线上的一点,OA=10cm,动点P从点A出发沿AB以2cm/s的速度移动,动点Q从点O出发沿OC以1cm/s的速度移动,如果点P,Q同时出发,用t(s)表示移动的时间,当t=$\frac{10}{3}$或10s时,△POQ是等腰三角形;当t=$\frac{20}{3}$s时,△POQ是直角三角形.
分析 根据△POQ是等腰三角形,分两种情况进行讨论:点P在AO上,或点P在BO上;根据△POQ是直角三角形,分两种情况进行讨论:PQ⊥AB,或PQ⊥OC,据此进行计算即可.
解答 解:如图,当PO=QO时,△POQ是等腰三角形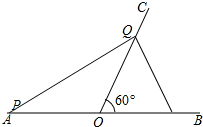
∵PO=AO-AP=10-2t,OQ=1t
∴当PO=QO时,10-2t=t
解得t=$\frac{10}{3}$;
如图,当PO=QO时,△POQ是等腰三角形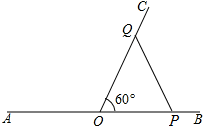
∵PO=AP-AO=2t-10,OQ=1t
∴当PO=QO时,2t-10=t
解得t=10;
如图,当PQ⊥AB时,△POQ是直角三角形,且QO=2OP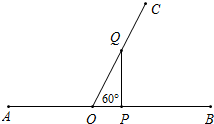
∵PO=AP-AO=2t-10,OQ=1t,
∴当QO=2OP时,t=2×(2t-10)
解得t=$\frac{20}{3}$;
如图,当PQ⊥OC时,△POQ是直角三角形,且2QO=OP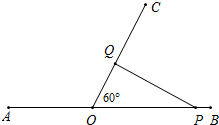
∵PO=AP-AO=2t-10,OQ=1t,
∴当2QO=OP时,2t=2t-10
方程无解.
故答案为:$\frac{10}{3}$或10;$\frac{20}{3}$
点评 本题主要考查了等腰三角形的性质以及直角三角形的性质,解决问题的关键是进行分类讨论,分类时注意不能遗漏,也不能重复.

练习册系列答案
相关题目
3.
| 抛物线 | 开口方向 | 顶点坐标 | 对称轴 |
| y=3(x-2)2+4 | 向上 | (2,4) | x=2 |
| y=(x+2)2 | 向上 | (-2,0) | x=-2 |
| y=-$\frac{1}{3}{x}^{2}$+5 | 向下 | (0,5) | x=0 |
| y=y=$\frac{1}{6}(x+3)^{2}+1$ | $\frac{1}{6}(x+3)^{2}+1$向下 | (-3,1) | x=-3 |
 如图,分别以锐角△ABC的边AB、BC、CA为斜边向外作等腰Rt△DAB、等腰Rt△EBC、等腰Rt△FAC.
如图,分别以锐角△ABC的边AB、BC、CA为斜边向外作等腰Rt△DAB、等腰Rt△EBC、等腰Rt△FAC. 如图,直线AB、CD被直线EF所截,且AB∥CD,FG⊥EF于点F,判断∠BEF与∠DFG之间存在什么关系?并说明理由.
如图,直线AB、CD被直线EF所截,且AB∥CD,FG⊥EF于点F,判断∠BEF与∠DFG之间存在什么关系?并说明理由. 如图,抛物线y=ax2+bx+c经过点A(-1,2),顶点C的坐标为(1,-2),与y轴的交点为点B.
如图,抛物线y=ax2+bx+c经过点A(-1,2),顶点C的坐标为(1,-2),与y轴的交点为点B.