题目内容
 如图,AB是⊙O的直径,点C在⊙O上,CD与⊙O相切,BD∥AC.
如图,AB是⊙O的直径,点C在⊙O上,CD与⊙O相切,BD∥AC.(1)图中∠OCD=
(2)⊙O的半径为3,AC=4,求CD的长.
考点:切线的性质,相似三角形的判定与性质
专题:几何综合题
分析:(1)根据切线的性质定理,即可解答;
(2)首先证明△ABC∽△CDB,利用相似三角形的对应边的比相等即可求解.
(2)首先证明△ABC∽△CDB,利用相似三角形的对应边的比相等即可求解.
解答: 解:(1)∵CD与⊙O相切,
解:(1)∵CD与⊙O相切,
∴OC⊥CD,(圆的切线垂直于经过切点的半径)
∴∠OCD=90°;
故答案是:90,圆的切线垂直于经过切点的半径;
(2)连接BC.
∵BD∥AC,
∴∠CBD=∠OCD=90°,
∴在直角△ABC中,
BC=
=
=2
,
∠A+∠ABC=90°,
∵OC=OB,
∴∠BCO=∠ABC,
∴∠A+∠BCO=90°,
又∵∠OCD=90°,
即∠BCO+∠BCD=90°,
∴∠BCD=∠A,
又∵∠CBD=∠ACB,
∴△ABC∽△CDB,
∴
=
,
∴
=
,
解得:CD=3
.
 解:(1)∵CD与⊙O相切,
解:(1)∵CD与⊙O相切,∴OC⊥CD,(圆的切线垂直于经过切点的半径)
∴∠OCD=90°;
故答案是:90,圆的切线垂直于经过切点的半径;
(2)连接BC.
∵BD∥AC,
∴∠CBD=∠OCD=90°,
∴在直角△ABC中,
BC=
| AB2-AC2 |
| 62-42 |
| 5 |
∠A+∠ABC=90°,
∵OC=OB,
∴∠BCO=∠ABC,
∴∠A+∠BCO=90°,
又∵∠OCD=90°,
即∠BCO+∠BCD=90°,
∴∠BCD=∠A,
又∵∠CBD=∠ACB,
∴△ABC∽△CDB,
∴
| CD |
| AB |
| BC |
| AC |
∴
| CD |
| 6 |
2
| ||
| 4 |
解得:CD=3
| 5 |
点评:本题考查了切线的性质定理以及相似三角形的判定与性质,证明两个三角形相似是本题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
我国吐鲁番盆地最低点的海拔是-a(a>0)米,死海湖面的海拔更低为-b(b>0)米,则死海湖面的海拔比吐鲁番盆地最低点的海拔低( )米.
| A、a+b | B、-b-a |
| C、-b+a | D、-a+b |
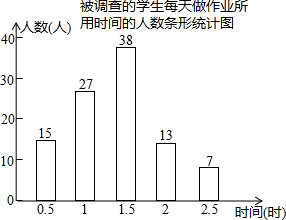 某校学生会为了解本校学生每天做作业所用时间情况,采用问卷的方式对一部分学生进行调查,在确定调查对象时,大家提出以下几种方案:
某校学生会为了解本校学生每天做作业所用时间情况,采用问卷的方式对一部分学生进行调查,在确定调查对象时,大家提出以下几种方案: 如图,在矩形ABCD中,对角线AC、BD相交于点O,EF是OA的中垂线,分别交AD、OA于点E、F.若AB=6cm,BC=8cm,则△DEO的周长=
如图,在矩形ABCD中,对角线AC、BD相交于点O,EF是OA的中垂线,分别交AD、OA于点E、F.若AB=6cm,BC=8cm,则△DEO的周长=