题目内容
7. 如图,在Rt△ABC中,∠ACB=90°,AB=6,若以AB边和BC边向外作等腰直角三角形AFC和等腰直角三角形BEC.若△BEC的面积为S1,△AFC的面积为S2,则S1+S2=( )
如图,在Rt△ABC中,∠ACB=90°,AB=6,若以AB边和BC边向外作等腰直角三角形AFC和等腰直角三角形BEC.若△BEC的面积为S1,△AFC的面积为S2,则S1+S2=( )| A. | 4 | B. | 9 | C. | 18 | D. | 36 |
分析 解:由勾股定理求出BC2+AC2=AB2=36,由等腰直角三角形的性质和勾股定理得出BE=CE=$\frac{\sqrt{2}}{2}$BC,AF=FC=$\frac{\sqrt{2}}{2}$AC,得出S1+S2=$\frac{1}{2}$BE2+$\frac{1}{2}$AF2=$\frac{1}{4}$(BC2+AC2),即可得出结果.
解答 解:∵∠ACB=90°,AB=6,
∴BC2+AC2=AB2=62=36,
∵△BEC和△AFC是等腰直角三角形,
∴BE=CE=$\frac{\sqrt{2}}{2}$BC,AF=FC=$\frac{\sqrt{2}}{2}$AC,
∴S1+S2=$\frac{1}{2}$BE2+$\frac{1}{2}$AF2=$\frac{1}{2}$×($\frac{\sqrt{2}}{2}$BC)2+$\frac{1}{2}$×($\frac{\sqrt{2}}{2}$AC)2=$\frac{1}{4}$(BC2+AC2)=$\frac{1}{4}$×36=9;
故选:B.
点评 本题考查了勾股定理、等腰直角三角形的性质、三角形面积的计算方法;熟练掌握勾股定理和等腰直角三角形的性质是解决问题的关键.

练习册系列答案
 优等生题库系列答案
优等生题库系列答案
相关题目
2.若a<$\sqrt{20}$<b,其中a,b是两个连续的整数,则a+b=( )
| A. | 6 | B. | 7 | C. | 8 | D. | 9 |
 按如图所示的程序计算,若开始输入的x的值为24,我们发现第一次得到的结果为12,第2次得到的结果为6,…,第2013次得到的结果为3.
按如图所示的程序计算,若开始输入的x的值为24,我们发现第一次得到的结果为12,第2次得到的结果为6,…,第2013次得到的结果为3. 如图,∠1=∠2,PD⊥OA,PE⊥OB,垂足分别是点D,E,则PE=PD(图中相等的线段,只写一对)
如图,∠1=∠2,PD⊥OA,PE⊥OB,垂足分别是点D,E,则PE=PD(图中相等的线段,只写一对)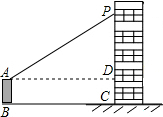 某消防队员进行消防演练,在模拟现场,有一建筑物发生了火灾,消防车到达后,发现最多只能靠近建筑物12米,即AD=BC=12米,此时建筑物中距离地面11.8米高的P处有一被困人员需要救援,已知消防云梯底部A距离地面2.8米,即AB=2.8米,则消防车的云梯至少要伸长15米.
某消防队员进行消防演练,在模拟现场,有一建筑物发生了火灾,消防车到达后,发现最多只能靠近建筑物12米,即AD=BC=12米,此时建筑物中距离地面11.8米高的P处有一被困人员需要救援,已知消防云梯底部A距离地面2.8米,即AB=2.8米,则消防车的云梯至少要伸长15米.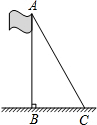 数学综合实验课上,同学们在测量学校旗杆的高度的时候发现:将旗杆顶端升旗用的绳子垂到地面还多2米,当把绳子的下端拉开8米后,下端刚好接触到地面,且绳子处于绷直状态.根据以上数据,计算旗杆的高度和升旗用的绳子的长度.
数学综合实验课上,同学们在测量学校旗杆的高度的时候发现:将旗杆顶端升旗用的绳子垂到地面还多2米,当把绳子的下端拉开8米后,下端刚好接触到地面,且绳子处于绷直状态.根据以上数据,计算旗杆的高度和升旗用的绳子的长度.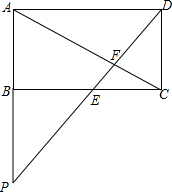 如图,已知四边形ABCD是矩形,求证:DF2=EF•FP.
如图,已知四边形ABCD是矩形,求证:DF2=EF•FP.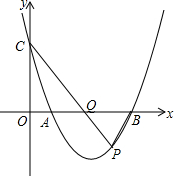 已知抛物线y=$\frac{3}{4}$x2-$\frac{15}{4}$x+3交x轴于A、B点,交y轴于点C,点P为x轴下方抛物线上一点,CP交x轴于点Q,当S△ACQ=S△PBQ,求点P的坐标.
已知抛物线y=$\frac{3}{4}$x2-$\frac{15}{4}$x+3交x轴于A、B点,交y轴于点C,点P为x轴下方抛物线上一点,CP交x轴于点Q,当S△ACQ=S△PBQ,求点P的坐标.