Question

5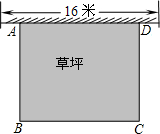．如图所示，某幼儿园有一道长为16米的墙，计划用32米长的围栏利用一面墙如图围成一个矩形草坪ABCD．设该矩形草坪AB边的长为x米，面积为y平方米．
（1）求出y与x的函数关系式并写出x的取值范围；
（ 2）如果所围成的矩形草坪面积为120平方米，试求AB边的长；
（3）按题目的设计要求，不能（填“能”或“不能”）围成面积为140平方米的矩形草坪．

Answer 1

分析 （1）利用矩形的面积计算公式得出y与x的函数关系式即可；
（2）利用（1）列出一元二次方程求解；
（3）利用（1）建立一元二次方程，由根的判别式就可以求出结论．

解答 解：（1）AB长为xm，则BC为（32-2x）m，
由题意得y=x（32-2x）=-2x²+32x（0＜x≤8）；

（2）由题意得 x（32-2x）=120，
解得x=6或x=10，
当x=6时，32-2x=20＞16，不合题意，舍去，
当x=10时，32-2x=12＜16，符合题意．
答：该矩形草坪BC边的长为12米；

（3）由题意得 x（32-2x）=140
∴x²-16x+70=0，
∴△=（-16）²-4×1×70=-240＜0，
∴此方程无实数根，
∴不能围成面积是140平方米的矩形草坪ABCD．

点评 本题考查了一元二次方程的应用，表示出矩形草坪的长和宽，利用矩形的面积建立关系式与方程是解题的关键．