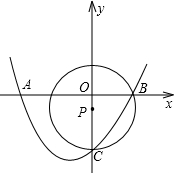
题目内容
 如图,抛物线y=
如图,抛物线y=| 2 |
| 3 |
| 2 |
| 3 |
| 3 |
| 3 |
| 2 |
(1)求抛物线的解析式;
(2)D在抛物线上,且C、D两点关于抛物线的对称轴对称,问直线BD是否经过圆心P?并说明理由;
(3)设直线BD交⊙P于另一点E,求经过点E和⊙P的切线的解析式.
分析:(1)将点C的坐标代入抛物线解析式即可求得c的值;
(2)已知D点坐标,可求直线BD的解析式,连接BP,设⊙P的半径为r,求出r,OP的值即可.
(3)过点E作EF⊥y轴于F,可求得△OPB≌△FPE,求出点P的坐标.然后由射影定理求得PE2=PF•PN,根据此关系式求解.
(2)已知D点坐标,可求直线BD的解析式,连接BP,设⊙P的半径为r,求出r,OP的值即可.
(3)过点E作EF⊥y轴于F,可求得△OPB≌△FPE,求出点P的坐标.然后由射影定理求得PE2=PF•PN,根据此关系式求解.
解答:解:(1)∵抛物线y=
x2+
x+c经过点C(0,-
),
∴c=-
,
∴该抛物线的解析式为y=
x2+
x-
;
(2)∵抛物线的解析式为y=
x2+
x-
,
∴对称轴为x=-
=-
.
又∵C(0,-
),C、D两点关于抛物线的对称轴对称,
∴D(-
,-
).
令
x2+
x-
=0,
解得,x1=-
,x2=
,
即A(-
,0)、B(
,0).
易求直线BD的解析式为:y=
x-
.
设⊙P的半径为r.则在直角△OBP中,根据勾股定理知BP2=OB2+OP2,即r2=(
)2+(
-r)2,
解得,r=1,则OP=OC-r=
-1=
.
∴P(0,
).
点P的坐标满足直线BD的解析式y=
x-
.即直线BD经过圆心P;
(3)过点E作EF⊥y轴于F,得△OPB≌△FPE,则E(-
,-1).
设经过E点⊙P的切线l交y轴于点N.
则∠PEN=90°,EF⊥PN,
∴PE2=PF•PN(射影定理),
∴PN=2,N(0,-2.5),(11分)
∴切线l为:y=-
x-
.
| 2 |
| 3 |
| 2 |
| 3 |
| 3 |
| 3 |
| 2 |
∴c=-
| 3 |
| 2 |
∴该抛物线的解析式为y=
| 2 |
| 3 |
| 2 |
| 3 |
| 3 |
| 3 |
| 2 |
(2)∵抛物线的解析式为y=
| 2 |
| 3 |
| 2 |
| 3 |
| 3 |
| 3 |
| 2 |
∴对称轴为x=-
| ||||
2×
|
| ||
| 2 |
又∵C(0,-
| 3 |
| 2 |
∴D(-
| 3 |
| 3 |
| 2 |
令
| 2 |
| 3 |
2
| ||
| 3 |
| 3 |
| 2 |
解得,x1=-
3
| ||
| 2 |
| ||
| 2 |
即A(-
3
| ||
| 2 |
| ||
| 2 |

易求直线BD的解析式为:y=
| ||
| 3 |
| 1 |
| 2 |
设⊙P的半径为r.则在直角△OBP中,根据勾股定理知BP2=OB2+OP2,即r2=(
| ||
| 2 |
| 3 |
| 2 |
解得,r=1,则OP=OC-r=
| 3 |
| 2 |
| 1 |
| 2 |
∴P(0,
| 1 |
| 2 |
点P的坐标满足直线BD的解析式y=
| ||
| 3 |
| 1 |
| 2 |
(3)过点E作EF⊥y轴于F,得△OPB≌△FPE,则E(-
| ||
| 2 |
设经过E点⊙P的切线l交y轴于点N.
则∠PEN=90°,EF⊥PN,
∴PE2=PF•PN(射影定理),
∴PN=2,N(0,-2.5),(11分)
∴切线l为:y=-
| 3 |
| 5 |
| 2 |
点评:本题考查的是二次函数的综合应用.难度较大.解题时,要数形结合,以防将点D的坐标误写为(
,-
).
| 3 |
| 3 |
| 2 |

练习册系列答案
相关题目
 并说明理由;
并说明理由; 0)和y轴上的点C(0,-
0)和y轴上的点C(0,- 如图,抛物线
如图,抛物线 轴于点A.动点P在线段AB上从点A向点B以每秒
轴于点A.动点P在线段AB上从点A向点B以每秒 (2013•义乌市)如图,抛物线y=ax2+bx+c与x轴交于点A(-1,0),顶点坐标为(1,n),与y轴的交点在(0,2)、(0,3)之间(包含端点),则下列结论:
(2013•义乌市)如图,抛物线y=ax2+bx+c与x轴交于点A(-1,0),顶点坐标为(1,n),与y轴的交点在(0,2)、(0,3)之间(包含端点),则下列结论: