��Ŀ����
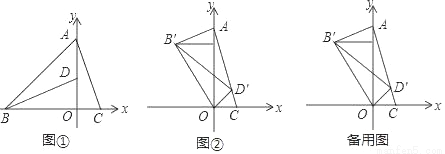
��ͼ�٣���ƽ��ֱ������ϵ�У���A��0��3������B����3��0������C��1��0������D��0��1������AB��AC��BD��
��1����֤��BD��AC��
��2����ͼ�ڣ�����BOD���ŵ�O��ת���õ���B��OD�䣬����D������AC��ʱ����AB��ij���
��3����ֱ��д�������е�B������꣮
��ϰ��ϵ�д�
�����Ŀ
��Ŀ����
��ͼ�٣���ƽ��ֱ������ϵ�У���A��0��3������B����3��0������C��1��0������D��0��1������AB��AC��BD��
��1����֤��BD��AC��
��2����ͼ�ڣ�����BOD���ŵ�O��ת���õ���B��OD�䣬����D������AC��ʱ����AB��ij���
��3����ֱ��д�������е�B������꣮
