题目内容
4.某设备的成本前年为1452元,今年的成本为1200元.设这两年该设备的年平均下降率为x,根据题意,所列方程为1452(1-x)2=1200.分析 则一年前生成的成本为1452(1-x)元,今年在1452(1-x)元的基础之又下降x,变为1452(1-x)(1-x)即1452(1-x)2元,进而可列出方程.
解答 解:设这两年成本年平均下降率为x,
则可得:1452(1-x)2=1200,
故答案为:1452(1-x)2=1200.
点评 此题主要考查了由实际问题抽象出一元二次方程,关键是掌握增长率问题的计算公式:变化前的量为a,变化后的量为b,平均变化率为x,则经过两次变化后的数量关系为a(1±x)2=b.

练习册系列答案
相关题目
12.小马虎在下面的计算中只做对了一道题,他做对的题目是( )
| A. | $\frac{m}{a}$+$\frac{m}{b}$=$\frac{2m}{ab}$ | B. | 1-$\frac{a-1}{a}$=-$\frac{1}{a}$ | C. | ($\frac{b}{a}$)2÷($\frac{a}{b}$)2=$\frac{{b}^{4}}{{a}^{4}}$ | D. | $\frac{-x-y}{x-y}$=-1 |
9.已知某数x,若比它的$\frac{2}{5}$大1的数是3,则可列出方程( )
| A. | $\frac{2}{5}$x+1=3 | B. | $\frac{5}{2}$x+1=3 | C. | $\frac{2}{5}$x-1=3 | D. | $\frac{5}{2}$x-1=3 |
14.一元一次不等式2(x+1)≥4的解集在数轴上表示为( )
| A. |  | B. |  | C. |  | D. |  |
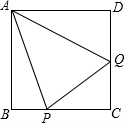 如图,正方形ABCD的边长为1,P、Q分别为边BC、CD上的点,连接PQ,若△CPQ的周长是2,求∠PAQ的度数.
如图,正方形ABCD的边长为1,P、Q分别为边BC、CD上的点,连接PQ,若△CPQ的周长是2,求∠PAQ的度数.