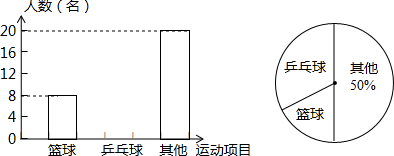
题目内容
19.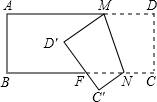 如图,把一张长方形纸片折叠后,点D、C分别落在Dˊ,Cˊ的位置.若∠AMDˊ=32°,则∠NFDˊ等于( )
如图,把一张长方形纸片折叠后,点D、C分别落在Dˊ,Cˊ的位置.若∠AMDˊ=32°,则∠NFDˊ等于( )| A. | 148° | B. | 108° | C. | 79° | D. | 122° |
分析 如图,首先运用翻折变换的性质证明∠D′MN=∠DMN,∠MNC′=∠MNC,借助∠AMD′=32°,求出∠DMN的度数,进而求出∠MNC、∠FNC′的度数;运用三角形外角的性质,即可解决问题.
解答  解:如图,∵四边形ABCD为矩形,
解:如图,∵四边形ABCD为矩形,
∴MD∥FN,∠DMN=∠MNF;
由题意得:∠D′MN=∠DMN,∠MNC′=∠MNC,
∵∠AMD′=32°,
∴∠DMN=$\frac{180°-32°}{2}$=74°,
∴∠MNC=180°-74°=106°,∠MNF=∠DMN=74°,
∴∠FNC′=106°-74°=32°,
∴∠NFD′=90°+32°=122°,
故选D.
点评 该题主要考查了翻折变换的性质、矩形的性质、直角三角形的性质等几何知识点及其应用问题;应牢固掌握翻折变换的性质、矩形的性质等几何知识点,这是灵活运用、解题的基础和关键.

练习册系列答案
相关题目
10.若反比例函数y=$\frac{3-m}{x}$,当x>0时,函数值y随x的增大而减小,则( )
| A. | m<0 | B. | m>0 | C. | m<3 | D. | m>3 |
7.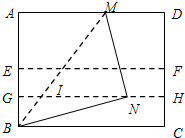 如图,对折矩形纸片ABCD,使BC与AD重合,折痕为EF,把纸片展平;再一次折叠纸片,使BC与EF重合,折痕为GH,把纸片展平;再一次折叠纸片,使点A落在GH上的点N处,并使折痕经过点B,折痕BM交GH于点I.若AB=4cm,则GI的长为( )
如图,对折矩形纸片ABCD,使BC与AD重合,折痕为EF,把纸片展平;再一次折叠纸片,使BC与EF重合,折痕为GH,把纸片展平;再一次折叠纸片,使点A落在GH上的点N处,并使折痕经过点B,折痕BM交GH于点I.若AB=4cm,则GI的长为( )
 如图,对折矩形纸片ABCD,使BC与AD重合,折痕为EF,把纸片展平;再一次折叠纸片,使BC与EF重合,折痕为GH,把纸片展平;再一次折叠纸片,使点A落在GH上的点N处,并使折痕经过点B,折痕BM交GH于点I.若AB=4cm,则GI的长为( )
如图,对折矩形纸片ABCD,使BC与AD重合,折痕为EF,把纸片展平;再一次折叠纸片,使BC与EF重合,折痕为GH,把纸片展平;再一次折叠纸片,使点A落在GH上的点N处,并使折痕经过点B,折痕BM交GH于点I.若AB=4cm,则GI的长为( )| A. | $\frac{\sqrt{10}}{4}$cm | B. | $\frac{3}{4}$cm | C. | $\frac{4}{5}$cm | D. | $\frac{\sqrt{15}}{5}$cm |
14.已知方程x2-5x+2=0的两个解分别为x1、x2,则x12+x22的值为( )
| A. | -7 | B. | -3 | C. | 21 | D. | 22 |
11.下列函数中,y值随x值的增大而增大的是( )
| A. | y=2x+3 | B. | y=-x+1 | C. | $y=\frac{1}{x}$ | D. | $y=-\frac{1}{x}$ |
 如图,AB、CD相交于点O,OE是∠AOC的平分线,∠BOD=70°,∠EOF=65°,则∠AOF的度数为30°.
如图,AB、CD相交于点O,OE是∠AOC的平分线,∠BOD=70°,∠EOF=65°,则∠AOF的度数为30°.