题目内容
在△ABC中，∠C=90°，BC=6，AC=8，以BC所在的直线为轴旋转一周，则所得的几何体的全面积为 ．
考点：圆锥的计算,点、线、面、体
专题：分类讨论
分析：易得此几何体为圆锥，那么表面积=底面积+侧面积=π×底面半径2+底面周长×母线长÷2．
解答：解：由题意知，∵在Rt△ABC中，∠ACB=90°，BC=6，AC=8，
∴BA2=CB2+AC2，
∴AB=10，
以AC为半径的圆的周长=2π×8=16π，底面面积=π×82=64π，
得到的圆锥的侧面面积=
×16π×10=80π，
表面积=80π+64π=144π，
故答案为：144π．
∴BA2=CB2+AC2，
∴AB=10，
以AC为半径的圆的周长=2π×8=16π，底面面积=π×82=64π，
得到的圆锥的侧面面积=
| 1 |
| 2 |
表面积=80π+64π=144π，
故答案为：144π．
点评：此题主要考查了圆锥侧面积的计算，关键是利用圆锥的侧面积=底面周长×母线长÷2得出．
练习册系列答案
53天天练系列答案
相关题目
如图，在直角坐标系xOy中，△ABC是等腰直角三角形，∠BAC=90°，A（1，0），B（0，2），抛物线y=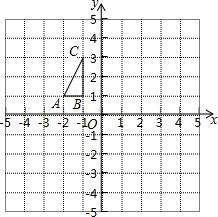
如图，每个小方格都是边长为1个单位长度的小正方形．
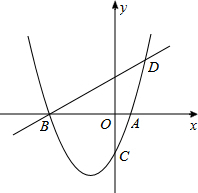如图，已知抛物线y=ax2+bx-2（a≠0）与x轴交于A、B两点，与y轴交与C点，直线BD交抛物线于点D，并且D（2，3），tan∠DBA=
如图，E、F在边长为2 的正方形ABCD内，使得△DCF为正三角形，△ABE为等腰直角三角形，则阴影部分的面积为