Question

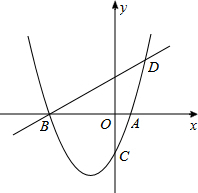如图，已知抛物线y=ax²+bx-2（a≠0）与x轴交于A、B两点，与y轴交与C点，直线BD交抛物线于点D，并且D（2，3），tan∠DBA=

1

2

．
（1）求抛物线的解析式；
（2）已知点M为抛物线上一动点，且在第三象限，顺次连接点B、M、C、A，求四边形BMCA面积的最大值．

Answer 1

考点：二次函数综合题

专题：

分析：（1）如答图1所示，利用已知条件求出点B的坐标，然后用待定系数法求出抛物线的解析式；
（2）如答图1所示，首先求出四边形BMCA面积的表达式，然后利用二次函数的性质求出其最大值．

解答：解：（1）如答图1所示，过点D作DE⊥x轴于点E，则DE=3，OE=2．
∵tan∠DBA=

DE

BE

=

1

2

，
∴BE=6，
∴OB=BE-OE=4，
∴B（-4，0）．
∵点B（-4，0）、D（2，3）在抛物线y=ax²+bx-2（a≠0）上，
∴

16a-4b-2=0 4a+2b-2=3

，
解得

a= 1 2 b= 3 2

，
∴抛物线的解析式为：y=

1

2

x²+

3

2

x-2．

（2）抛物线的解析式为：y=

1

2

x²+

3

2

x-2，
令x=0，得y=-2，∴C（0，-2），
令y=0，得x=-4或1，∴A（1，0）．
设点M坐标为（m，n）（m＜0，n＜0），
如答图1所示，过点M作MF⊥x轴于点F，则MF=-n，OF=-m，BF=4+m．
S_{四边形BMCA}=S_△BMF+S_梯形MFOC+S_△AOC
=

1

2

BF•MF+

1

2

（MF+OC）•OF+

1

2

OA•OC
=

1

2

（4+m）×（-n）+

1

2

（-n+2）×（-m）+

1

2

×1×2
=-2n-m+1
∵点M（m，n）在抛物线y=

1

2

x²+

3

2

x-2上，
∴n=

1

2

m²+

3

2

m-2，代入上式得：
S_{四边形BMCA}=-m²-4m+5=-（m+2）²+9，
∴当m=-2时，四边形BMCA面积有最大值，最大值为9．

点评：本题考查了二次函数的图象与性质、一次函数的图象与性质、待定系数法、图形面积计算等重要知识点，涉及考点众多，有一定的难度．第（2）问面积最大值的问题，利用二次函数的最值解决．