题目内容
如图，△ABC内有并排的n个相等的小正方形，它们组成的矩形内接于△ABC．已知BC=10，BC边上的高为6，则小正方形的边长等于考点：相似三角形的判定与性质,正方形的性质
专题：
分析：如图，过A作AD⊥BC，交EF于点G，根据相似三角形的性质可得到
=
，代入可求得EF的长，可得到答案．
| AG |
| AD |
| EF |
| BC |
解答：
解：如图，过A作AD⊥BC，交EF于点G，交BC于点D，
∵EF∥BC，
∴
=
，
设小正方形的边长为x，则AG=AD-x=6-x，EF=nx，
∴
=
，
解得x=
，即小正方形的边长为
，
故答案为：
．
解：如图，过A作AD⊥BC，交EF于点G，交BC于点D，∵EF∥BC，
∴
| AG |
| AD |
| EF |
| BC |
设小正方形的边长为x，则AG=AD-x=6-x，EF=nx，
∴
| 6-x |
| 6 |
| nx |
| 10 |
解得x=
| 30 |
| 3n+5 |
| 30 |
| 3n+5 |
故答案为：
| 30 |
| 3n+5 |
点评：本题主要考查相似三角形的性质，掌握相似三角形对应高的比等于相似比是解题的关键．
练习册系列答案
相关题目
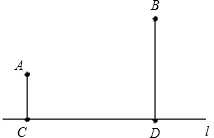如图，A、B是一条河l同侧的两个村庄，且A、B两个村庄到河的距离分别是3千米和5千米，两村庄之间的距离AB为2
如图，O是直线AB上一点，OD是∠AOC的平分线，OE⊥OD．OE是∠BOC的平分线吗？为什么？
如图，E、F、G、H分别是BD、BC、AC、AD的中点，且AB=CD．下列结论：①EH=FG，②EH=HG，③四边形EFGH是菱形，④EG⊥FH．其中正确的个数是（ ）