题目内容
19.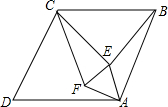 如图,在菱形ABCD中,∠D=60°,点E、F在菱形ABCD内部,△AEF为等边三角形.
如图,在菱形ABCD中,∠D=60°,点E、F在菱形ABCD内部,△AEF为等边三角形.(1)求证:BE=CF;
(2)若AE=6,BE=10,CE=8,求∠AEC的度数.
分析 (1)首先证明△ACD为等边三角形,从而得到AC=AB,然后根据菱形的性质和等边三角形的性质证明∠FAC=∠EAB,最后证明△CFA≌△BEA,从而可证得:BE=CF;
(2)首先利用勾股定理的逆定理证明△CEF为直角三角形,然后即可求得∠AEC的度数.
解答 证明:(1)连接AC.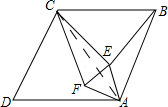
∵四边形ABCD是菱形,
∴DC=DA=AB=BC,∠DAC=∠CAB.
∵DC=DA,∠D=60°.
∴△DAC为等边三角形.
∴AC=AD,∠DAC=∠CAB=60°
∴AC=AB.
∵△EFA为等边三角形,
∴∠FAE=60°,FA=EA.
∴∠FAE-∠EAC=∠CAB-∠EAC,即∠FAC=∠EAB.
在△CFA和△BEA中,
$\left\{\begin{array}{l}{AC=AB}\\{∠FAC=∠EAB}\\{FA=EA}\end{array}\right.$,
∴△CFA≌△BEA.
∴BE=CF.
(2)∵BE=CF,
∴CF=10.
∵CF=10,EF=AE=6,CE=8.
∴CF2=EF2+CE2.
∴∠CEF=90°.
∵△EFA为等边三角形,
∴∠FEA=60°.
∴∠AEC=90°+60°=150°.
点评 本题主要考查的是勾股定理的逆定理、等边三角形的性质、全等三角形的性质和判定,证得△CFA≌△BEA是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
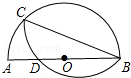 以半圆中的一条弦BC(非直径)为对称轴将弧BC折叠后与直径AB交于点D,若$\frac{AD}{DB}$=$\frac{2}{3}$,且AB=10,则CB的长为4$\sqrt{5}$.
以半圆中的一条弦BC(非直径)为对称轴将弧BC折叠后与直径AB交于点D,若$\frac{AD}{DB}$=$\frac{2}{3}$,且AB=10,则CB的长为4$\sqrt{5}$.
 如图,已知AB∥ED,∠B=50°,CN是∠BCE的平分线,CM⊥CN,求∠MCD的度数.
如图,已知AB∥ED,∠B=50°,CN是∠BCE的平分线,CM⊥CN,求∠MCD的度数.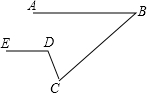 如图,已知AB∥DE,∠B=40°,∠EDC=110°,则∠C的度数为70°.
如图,已知AB∥DE,∠B=40°,∠EDC=110°,则∠C的度数为70°.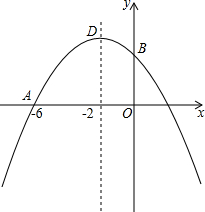 已知抛物线y=ax2-x+c过点A(-6,0),对称轴是直线x=-2,与y轴交于点B,顶点为D.
已知抛物线y=ax2-x+c过点A(-6,0),对称轴是直线x=-2,与y轴交于点B,顶点为D.