题目内容
3.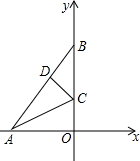 如图,平面直角坐标系中有一张三角形纸片AOB,其顶点A,B的坐标分别为A(-6,0),B(0,8),点O为坐标原点.
如图,平面直角坐标系中有一张三角形纸片AOB,其顶点A,B的坐标分别为A(-6,0),B(0,8),点O为坐标原点.(1)求边AB的长;
(2)点C是线段OB上一点,沿线段AC所在直线折叠△AOB,使得点O落在边AB上的点D处,求点C的坐标.
分析 (1)根据A与B的坐标确定出OA与OB的长,在直角三角形AOB中,利用勾股定理求出AB的长即可;
(2)由折叠的性质得到三角形ADC与三角形AOC全等,利用全等三角形对应边相等得到AD=AO,CD=CO,设OC=x,根据勾股定理列出关于x的方程,求出方程的解得到x的值,即可确定出C坐标.
解答 解:(1)∵A(-6,0),B(0,8),
∴OA=6,OB=8,
根据勾股定理得:AB=$\sqrt{{6}^{2}+{8}^{2}}$=10;
(2)设OC=x,由折叠的性质得:AD=AO=6,CD=OC=x,∠BDC=90°,
∴BD=AB-AD=4,BC=8-x,
在Rt△BDC中,根据勾股定理得:42+x2=(8-x)2,
解得:x=3,
则C的坐标为(0,3).
点评 此题属于一次函数综合题,涉及的知识有:坐标与图形性质,折叠的性质,勾股定理,熟练掌握性质及定理是解本题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
11.下列各式中,不能用平方差公式分解因式的是( )
| A. | x4-y4 | B. | 4m2+n2 | C. | $\frac{1}{144}$-x4 | D. | (a+b)2-81 |
18.解方程x-3(x-1)=5,去括号正确的是( )
| A. | x-3x-1=5 | B. | x-3x-3=5 | C. | x-3x+3=5 | D. | x-3x+1=5 |
12.定义:如果10b=n,那么称b为n的劳格数,记为b=d(n).
(1)根据劳格数的定义,可知:d(10)=1,d(102)=2,那么:d(103)=3.
(2)劳格数有如下运算性质:若m、n为正数,则d(mn)=d(m)+d(n);d($\frac{m}{n}$)=d(m)-d(n).
根据运算性质,填空:$\frac{{d({2^5})}}{d(2)}$=5,若d(3)=0.477,则d(9)=0.954,d(0.3)=-0.523.
(3)下表中与x数对应的劳格数d(x)有且只有两个是错误的,请找出错误的劳格数并改正.
(1)根据劳格数的定义,可知:d(10)=1,d(102)=2,那么:d(103)=3.
(2)劳格数有如下运算性质:若m、n为正数,则d(mn)=d(m)+d(n);d($\frac{m}{n}$)=d(m)-d(n).
根据运算性质,填空:$\frac{{d({2^5})}}{d(2)}$=5,若d(3)=0.477,则d(9)=0.954,d(0.3)=-0.523.
(3)下表中与x数对应的劳格数d(x)有且只有两个是错误的,请找出错误的劳格数并改正.
| x | 1.5 | 3 | 5 | 6 | 8 | 9 | 12 | 27 |
| d(x) | 3a-b+c | 2a-b | a+c | 1+a-b-c | 3-3a-3c | 4a-2b | 3-b-2c | 6a-3b |
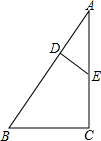 如图,已知在Rt△ABC中,∠C=90°,D、E分别为AB、AC边上的点,且$\frac{AD}{AE}$=$\frac{4}{5}$,连结DE,若AC=4,BC=3.求证:
如图,已知在Rt△ABC中,∠C=90°,D、E分别为AB、AC边上的点,且$\frac{AD}{AE}$=$\frac{4}{5}$,连结DE,若AC=4,BC=3.求证: