题目内容
3.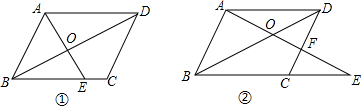 在?ABCD中,点E从点B开始沿BC方向向C点运动,如图①所示,连接AE交BD于点O,得到△AOD与△BOE始终相似.
在?ABCD中,点E从点B开始沿BC方向向C点运动,如图①所示,连接AE交BD于点O,得到△AOD与△BOE始终相似.(1)当E点运动到何处时,△AOD与△BOE的相似比为2:1?
(2)当E点运动到何处时,△AOD与△BOE全等?
(3)若E点到达C点后,继续沿着BC的方向向右运动,如图②所示,这时AE与CD的交点为F,且△ADF∽△ECF.试说明:当E点运动到某一点,使△ADF与△ECF全等时,点F在CD的什么位置?并求出这时△AOD与△BOE的相似比.
(4)在图②中,$\frac{CD}{CF}$=$\frac{BE}{CE}$的值是否一定?若一定,请求出这个值;若不一定,请说明理由.
分析 (1)根据△AOD与△BOE的相似比为2:1,求出AD与BE的关系,得到答案;
(2)根据全等三角形的性质求出E点运动的位置;
(3)根据全等三角形的性质求出AD与CE的关系,得到答案;
(4)根据题意可知CE是在变化的,而BC为定值,得出结论.
解答 解:(1)∵△AOD与△BOE的相似比为2:1,
∴$\frac{AD}{BE}$=$\frac{2}{1}$,又AD=BC,
∴E点运动到BC的中点时,△AOD与△BOE的相似比为2:1;
(2)∵△AOD与△BOE全等,
∴AD=BC,
∴点E与点C重合时,△AOD与△BOE全等;
(3)∵△ADF与△ECF全等,
∴DF=CF,则点F为CD的中点,
∴点F为CD的中点时,△ADF与△ECF全等,
∵△ADF与△ECF全等,∴AD=CE,
则AD=$\frac{1}{2}$BE,
∴△AOD与△BOE相似比为$\frac{1}{2}$;
(4)∵E点到达C点后,继续沿着BC的方向向右运动,
∴线段CE在逐渐增大,而线段BC不变,
∴$\frac{BE}{CE}$的值是不一定的.
点评 本题考查的是相似三角形的判定和性质,掌握判定定理和性质定理是解题的关键,注意三角形全等是三角形相似的一种特殊形式.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
6.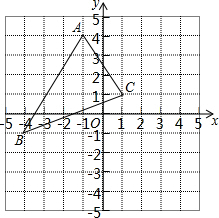 如图,若△ABC中任意一点P(x0,y0)经平移后对应点为P1(x0+5,y0-3),那么将△ABC作同样的平移得到△A1B1C1,则点A的对应点A1的坐标是( )
如图,若△ABC中任意一点P(x0,y0)经平移后对应点为P1(x0+5,y0-3),那么将△ABC作同样的平移得到△A1B1C1,则点A的对应点A1的坐标是( )
 如图,若△ABC中任意一点P(x0,y0)经平移后对应点为P1(x0+5,y0-3),那么将△ABC作同样的平移得到△A1B1C1,则点A的对应点A1的坐标是( )
如图,若△ABC中任意一点P(x0,y0)经平移后对应点为P1(x0+5,y0-3),那么将△ABC作同样的平移得到△A1B1C1,则点A的对应点A1的坐标是( )| A. | (4,1) | B. | (9,-4) | C. | (-6,7) | D. | (-1,2) |
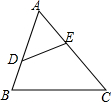 如图,已知D,E分别是△ABC的AB,AC边上的点,且AD=5,BD=3,AE=4,CE=6,求证:∠ADE=∠C.
如图,已知D,E分别是△ABC的AB,AC边上的点,且AD=5,BD=3,AE=4,CE=6,求证:∠ADE=∠C.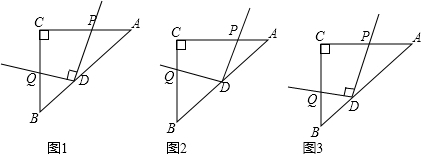
 如图:在△ABC中,AD、BE、CF是△ABC的高,交点为H,则△AHC的三边上高分别为HE,AF,CD.
如图:在△ABC中,AD、BE、CF是△ABC的高,交点为H,则△AHC的三边上高分别为HE,AF,CD.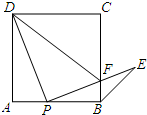 如图,点P是正方形ABCD边AB上一点(不与点A,B重合),连接PD并将线段PD绕点P顺时针方向旋转90°得到线段PE,PE交边BC于点F,连接BE,DF.
如图,点P是正方形ABCD边AB上一点(不与点A,B重合),连接PD并将线段PD绕点P顺时针方向旋转90°得到线段PE,PE交边BC于点F,连接BE,DF.