题目内容
6.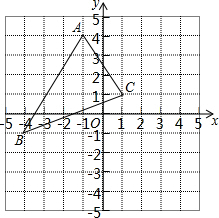 如图,若△ABC中任意一点P(x0,y0)经平移后对应点为P1(x0+5,y0-3),那么将△ABC作同样的平移得到△A1B1C1,则点A的对应点A1的坐标是( )
如图,若△ABC中任意一点P(x0,y0)经平移后对应点为P1(x0+5,y0-3),那么将△ABC作同样的平移得到△A1B1C1,则点A的对应点A1的坐标是( )| A. | (4,1) | B. | (9,-4) | C. | (-6,7) | D. | (-1,2) |
分析 首先根据坐标系可得A点坐标,再根据P点的坐标的变化规律可得A点的坐标的变化规律,进而可得答案.
解答 解:由坐标系可得A(-1,4),
∵△ABC中任意一点P(x0,y0)经平移后对应点为P1(x0+5,y0-3),
∴点A的对应点A1的坐标是(-1+5,4-3),即(4,1).
故选:A.
点评 此题主要考查了坐标与图形的变化--平移,关键是掌握横坐标,右移加,左移减;纵坐标,上移加,下移减.

练习册系列答案
相关题目
16.下列运算正确的是( )
| A. | x8÷x4=x2 | B. | t4÷(-t2)=t2 | C. | b2m÷bm=b2 | D. | (-m)6÷(-m)2=m4 |
14. 如图,∠A+∠B+∠C+∠D+∠E等于( )
如图,∠A+∠B+∠C+∠D+∠E等于( )
 如图,∠A+∠B+∠C+∠D+∠E等于( )
如图,∠A+∠B+∠C+∠D+∠E等于( )| A. | 180° | B. | 360° | C. | 540° | D. | 720° |
1.下列事件是必然事件的是( )
| A. | 抛一枚硬币,正面朝上 | |
| B. | 打开电视,正在播放动画片 | |
| C. | 3个人分成两组,一定有2个人分在一组 | |
| D. | 随意掷两个均匀的骰子,上面的点数之和为6 |
18.直线AB与x轴交于点A(1,0),与y轴交于点B(0,-2),点C在直线AB上,且S△BOC=2,则点C的坐标是( )
| A. | (-2,-2) | B. | (-2,-6) | C. | (2,2) | D. | (2,2)或(-2,-6) |
15.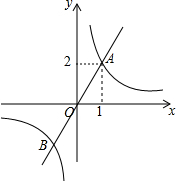 如图,函数y1=$\frac{k_1}{x}$与y2=k2x的图象相交于点A(1,2)和点B,当y1<y2时,自变量x的取值范围是( )
如图,函数y1=$\frac{k_1}{x}$与y2=k2x的图象相交于点A(1,2)和点B,当y1<y2时,自变量x的取值范围是( )
 如图,函数y1=$\frac{k_1}{x}$与y2=k2x的图象相交于点A(1,2)和点B,当y1<y2时,自变量x的取值范围是( )
如图,函数y1=$\frac{k_1}{x}$与y2=k2x的图象相交于点A(1,2)和点B,当y1<y2时,自变量x的取值范围是( )| A. | -1<x<0或x>1 | B. | x<-1或0<x<1 | C. | x>1 | D. | -1<x<0 |
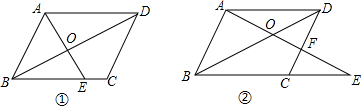 在?ABCD中,点E从点B开始沿BC方向向C点运动,如图①所示,连接AE交BD于点O,得到△AOD与△BOE始终相似.
在?ABCD中,点E从点B开始沿BC方向向C点运动,如图①所示,连接AE交BD于点O,得到△AOD与△BOE始终相似.