题目内容
2．
如图，△ABC中，CA=CB，D为△ABC内一点，∠1=∠2，若∠C=40°，求∠ADB的度数．
分析 根据等腰三角形的性质求得∠CAB=∠CBA=70°，然后根据三角形内角和定理得出∠ADB=180°-（∠1+∠ABD）=180°-（∠2+∠ABD）=180°-∠CBA=180°-70°=110°．
解答 解：∵CA=CB，
∴∠CAB=∠CBA，
∵∠C=40°，
∴∠CAB=∠CBA=$\frac{180°-40°}{2}$=70°，
∵∠ADB=180°-（∠1+∠ABD），∠1=∠2，
∴∠ADB=180°-（∠2+∠ABD）=180°-∠CBA=180°-70°=110°．
点评 本题考查了等腰三角形的性质，三角形内角和定理，熟练掌握性质定理是解题的关键．
练习册系列答案
云南师大附小一线名师提优作业系列答案
相关题目
13．2015年8月20日《互联网周刊》报道，近期余额宝收益率持续下跌，从两年前年化收益率保持在6%以上到今日不足3.5%，玲玲在余额宝中存入约1.7万元，下表是玲玲对余额宝一周内收益率变化情况的记录（增加为正，减少为负）．
注：①表中记录的数据为媒体拿的收益与前一天收益的变化量；
②上星期日的收益为1.5元．
（1）请你通过计算说明该星期日与上星期日相比，收益增加了还是减少了？如果增加了，求出增加的钱数，如果减少了，求出减少的钱数．
（2）求这一周玲玲总共收益的钱数．
| 时间 | 星期一 | 星期二 | 星期三 | 星期四 | 星期五 | 星期六 | 星期日 |
| 收益变化/元 | +0.01 | +0.01 | -0.02 | -0.04 | -0.01 | +0.01 | +0.03 |
②上星期日的收益为1.5元．
（1）请你通过计算说明该星期日与上星期日相比，收益增加了还是减少了？如果增加了，求出增加的钱数，如果减少了，求出减少的钱数．
（2）求这一周玲玲总共收益的钱数．
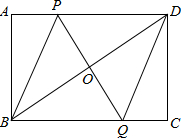如图，在矩形ABCD中，点P是线段AD上一动点，O为BD的中点，PO的延长线交BC于Q．