题目内容
19. 已知抛物线的顶点为坐标原点,且经过点A(-1,1)
已知抛物线的顶点为坐标原点,且经过点A(-1,1)(1)求抛物线的解析式;
(2)作出抛物线(大致图象);
(3)若抛物线与直线y=x+m有交点,求实数m的取值范围.
分析 (1)设抛物线的解析式y=ax2,代入点A(-1,1)求得解析式即可;
(2)利用解析式作出图象即可;
(3)与直线y=x+m联立方程,利用根的判别式判定m的取值范围即可.
解答 解:(1)设抛物线的解析式y=ax2,代入点A(-1,1)得,
a=1,
因此抛物线的解析式y=x2;
(2)图象如下:
(3)由题意得:
x2=x+m,
x2-x-m=0
△=1+4m≥0,
解得:m≥$\frac{1}{4}$.
点评 此题考查待定系数法求函数解析式,二次函数与一次函数的交点问题,掌握基本的方法是解决问题的关键.

练习册系列答案
相关题目
10.下列说法:①全等三角形的形状相同、大小相等;②全等三角形的对应边相等;③全等三角形的对应角相等;④全等三角形的周长相等,面积不相等,其中正确的为( )
| A. | ①②③④ | B. | ①②③ | C. | ①②④ | D. | ①②③④ |
4.下列说法中,正确的是( )
| A. | 平方是它本身的数是正数 | B. | 绝对值是它本身的数是零 | ||
| C. | 倒数是它本身的数是±1 | D. | 立方是它本身的数是±1 |
11. 由几个相同的小立方块组成一个立体图形,如图是从不同方向看到它的图形,小立方块的个数是( )
由几个相同的小立方块组成一个立体图形,如图是从不同方向看到它的图形,小立方块的个数是( )
 由几个相同的小立方块组成一个立体图形,如图是从不同方向看到它的图形,小立方块的个数是( )
由几个相同的小立方块组成一个立体图形,如图是从不同方向看到它的图形,小立方块的个数是( )| A. | 3个 | B. | 4个 | C. | 5个 | D. | 6个 |
9.“a与b的差的2倍”用代数式表示为( )
| A. | a-2b | B. | 2a-b | C. | 2(a-b) | D. | $\frac{a-b}{2}$ |
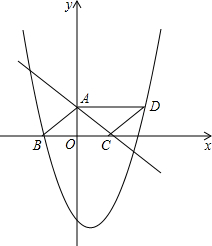 如图,△ABC是以BC为底边的等腰三角形,点A、C分别是一次函数y=-$\frac{3}{4}$x+3的图象与y轴、x轴的交点,点B、点D在二次函数y=$\frac{1}{8}$x2+bx+c的图象上,且四边形ABCD是平行四边形.
如图,△ABC是以BC为底边的等腰三角形,点A、C分别是一次函数y=-$\frac{3}{4}$x+3的图象与y轴、x轴的交点,点B、点D在二次函数y=$\frac{1}{8}$x2+bx+c的图象上,且四边形ABCD是平行四边形.