题目内容
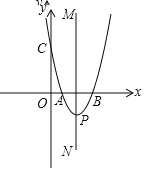
【题目】平面直角坐标系![]() 中(如图),已知抛物线
中(如图),已知抛物线![]() 经过点
经过点![]() 和
和![]() ,与y轴相交于点C,顶点为P.
,与y轴相交于点C,顶点为P.
(1)求这条抛物线的表达式和顶点P的坐标;
(2)点E在抛物线的对称轴上,且![]() ,求点E的坐标;
,求点E的坐标;
(3)在(2)的条件下,记抛物线的对称轴为直线MN,点Q在直线MN右侧的抛物线上,![]() ,求点Q的坐标.
,求点Q的坐标.
【答案】(1)![]() ,顶点P的坐标为
,顶点P的坐标为![]() ;(2)E点坐标为
;(2)E点坐标为![]() ;(3)Q点的坐标为
;(3)Q点的坐标为![]() .
.
【解析】
(1)利用交点式写出抛物线解析式,把一般式配成顶点式得到顶点P的坐标;
(2)设![]() ,根据两点间的距离公式,利用
,根据两点间的距离公式,利用![]() 得到
得到![]() ,然后解方程求出t即可得到E点坐标;
,然后解方程求出t即可得到E点坐标;
(3)直线![]() 交
交![]() 轴于
轴于![]() ,作
,作![]() 于
于![]() ,如图,利用
,如图,利用![]() 得到
得到![]() ,设
,设![]() ,则
,则![]() ,再在
,再在![]() 中利用正切的定义得到
中利用正切的定义得到![]() ,即
,即![]() ,然后解方程求出m即可得到Q点坐标.
,然后解方程求出m即可得到Q点坐标.
解:(1)抛物线解析式为![]() ,
,
即![]() ,
,
![]() ,
,
![]() 顶点P的坐标为
顶点P的坐标为![]() ;
;
(2)抛物线的对称轴为直线![]() ,
,
设![]() ,
,
![]() ,
,
![]() ,解得
,解得![]() ,
,
![]() E点坐标为
E点坐标为![]() ;
;
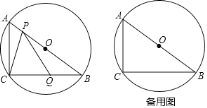
(3)直线![]() 交x轴于F,作MN⊥直线x=2于H,如图,
交x轴于F,作MN⊥直线x=2于H,如图,
![]() ,
,
而![]() ,
,
![]() ,
,
设![]() ,则
,则![]() ,
,
在![]() 中,
中,![]() ,
,
![]() ,
,
整理得![]() ,解得
,解得![]() (舍去),
(舍去),![]() ,
,
![]() Q点的坐标为
Q点的坐标为![]() .
.


练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目